Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.3 - Ex. 19
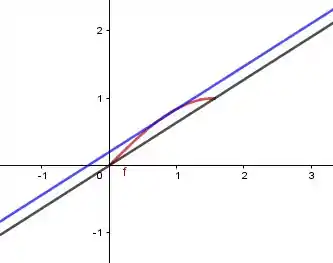
A interpretação geométrica do teorema do valor médio é que para um valor adequado de no intervalo aberto , a reta tangente à curva no ponto é paralela à secante que passa pelos pontos e . Ache um valor de que satisfaça a conclusão do teorema do valor médio, faça um esboço do gráfico no intervalado fechado e coloque no gráfico as retas tangente e secante.
Passo 1
Como é uma função trigonométrica, ela será contínua para todo real, em particular será continua no intervalo . Mesma justificativa garante ser derivável em . Logo, pelo teorema do valor médio, existe tal que:
Pela definição de derivada temos:
Assim:
Passo 2
Substituindo este valor de na função temos:
Temos também:
Queremos encontrar a reta que seja tangente a passando pelo ponto e que seja paralela à reta que passa por e. A reta que que passa por esses pontos terá inclinação:
Queremos encontrar a reta que passa por e tenha inclinação . Assim:
Resposta
Portanto, satisfaz o teorema do valor médio. Esboço da função no intervalo , das retas tangente e secante a em :
