Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 49
Encontre a área da região entre o eixo e a curva com .
Passo 1
Vamos visualizar a região, que é acima do eixo e abaixo da curva com :
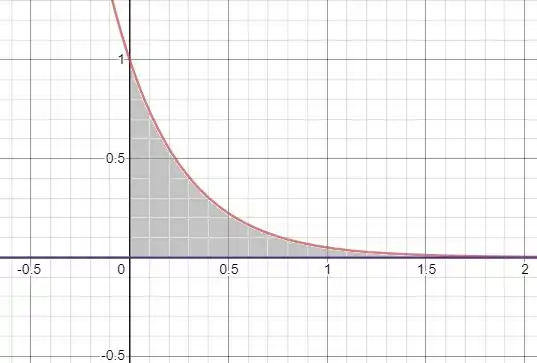
Temos que a área vai ser a integral:
Onde o limite de integração vai de até infinito, e devemos integrar a função da curva.
Passo 2
Temos aqui que é contínua no intervalo , exceto por uma descontinuidade infinita em , então a integral imprópria de no intervalo é definida por:
Vamos agora substituir os limites de integração e a função:
Passo 3
Vamos calcular a integral do limite, vamos calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Vamos fazer uma substituição:
Próximo passo é substituir na integral:
Passo 4
Aqui, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Lembre de voltar a variável original , é só substituir de volta o que você usou lá no começo:
Passo 5
Pronto, já encontramos a integral indefinida, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Agora vamos voltar a integral:
Passo 6
Agora vamos calcular a integral original:
Pronto, temos que a área da região é de .