Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.2 - Ex. 7

  1. Encontre uma equação para a família de funções lineares com inclinação 2 e esboce os gráficos de vários membros da família.

  2. Encontre uma equação para a família de funções lineares tais que f 2 = 1 e esboce os gráficos de vários membros da família.

  3. Qual função pertence a ambas as famílias?

Passo 1

E aí meus amigos, tudo bom? Essa aqui é uma questão onde temos que conseguir descrever uma família de funções.

Uma "família de funções" é um conjunto de funções relacionadas por uma característica comum, como uma propriedade específica ou parâmetro.

A gente tem que basicamente achar um conjunto de retas que descreva os casos em cada um dos itens, então dada algumas condições, iremos encontrar outras retas que compartilhem dessas mesmas condições.

Em certos momentos utilizar a forma:

y = m x + b

Onde m é o coeficiente angular da reta, é o que influencia no quão inclinada nossa reta será e se ela será crescente m > 0 ou descrecente m < 0 .

b é o coeficiente linear da reta, é onde a nossa reta irá tocar o eixo y .

Também temos a forma:

y - y 1 = m x - x 1

Em que ( x 1 , y 1 ) é o ponto que obrigatoriamente a gente quer que nossa reta passe.

Passo 2

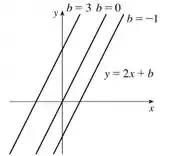
  1. Podemos escrever todas as funções lineares (ou seja, funções cujo gráfico é uma reta) com inclinação 2 com a equação:

    2. y = 2 x + b

    A constante que acompanha a incógnita é a inclinação, enquanto o b representa onde a reta corta o eixo vertical y .

    Desenhando várias retas com vários b diferentes, teremos o nosso esboço com os vários membros dessa família de funções. Dá uma olhada no que temos aqui:

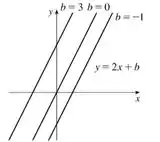
    temos então a mesma inclinação, mas por termos b diferentes, a reta toca o eixo y em pontos diferentes.

  2. Nesse item, vamos usar a equação da reta:

    3. y - y 1 = m   .   ( x - x 1 )

    Onde m é a inclinação da reta e o ponto ( x 1 ,   y 1 ) é um ponto dessa reta.

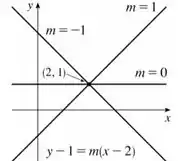
    O enunciado diz que as nossas retas devem satisfazer a condição f 2 = 1 , ou seja, querem que tenhamos o ponto ( 2,1 ) na nossa reta. Colocando esse ponto na nossa equação, teremos:

    y - 1 = m ∙   ( x - 2 )

    y - 1 = m ∙   x - 2 m

    y = m ∙   x - 2 m + 1

    y = m ∙ x + ( 1 - 2 m )

    A partir dessa expressão, dá pra ver que a família de funções que procuramos são um conjunto de retas, todas passando pelo mesmo ponto ( 2,1 ) , mas com inclinações diferentes. Dá uma olhada em como ficará o nosso gráfico, mostrando alguns possíveis valores de m :

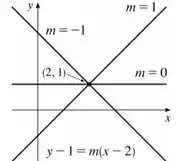
    Passo 3

  3. Já que queremos uma função que pertença a ambas as famílias, precisamos de uma reta que tenha uma inclinação m = 2 e passe pelo ponto ( 2,1 ) .

Com a equação da reta que aparece no passo anterior, rapidinho a gente mata essa! Olha só:

y - y 1 = m ∙   x - x 1

Substituindo o ponto:

y - 1 = 2 ∙ ( x - 2 )

y - 1 = 2 x - 4

y = 2 x - 3

Pronto! Essa é a nossa função resposta.

Resposta

  1. y = 2 x + b

  2. y = m   .   x + ( 1 - 2 m )

  3. y = 2 x - 3
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando uma ferramenta gráfica, traçar as curvas definidas pelas equações dadas, identificando as que representam o gráfico de uma função y = f ( x ) . Neste caso, determine a função, o domínio e o con
Usando uma ferramenta gráfica, traçar as curvas definidas pelas equações dadas, identificando as que representam o gráfico de uma função y = f ( x ) . Neste caso, determine a função, o domínio e o con
Usando uma ferramenta gráfica, traçar as curvas definidas pelas equações dadas, identificando as que representam o gráfico de uma função y = f ( x ) . Neste caso, determine a função, o domínio e o con
Usando uma ferramenta gráfica, traçar as curvas definidas pelas equações dadas, identificando as que representam o gráfico de uma função y = f ( x ) . Neste caso, determine a função, o domínio e o con
Usando uma ferramenta gráfica, traçar as curvas definidas pelas equações dadas, identificando as que representam o gráfico de uma função y = f ( x ) . Neste caso, determine a função, o domínio e o con