Encontre uma equação da(s) tangente(s) à curva no ponto dado. Então, plote a curva e a(s) tangente(s).
Passo 1
O exercício quer que você encontre a equação da reta tangente à curva parametrizada dada.
Quando falamos sobre equação da reta tangente, estamos falando sobre derivadas. A equação de uma reta tangente a uma curva é dada por:
Em que é o ponto que queremos que a nossa reta seja tangente, e costuma ser dado na questão, no nosso caso é o ponto:
Já é o coeficiente angular da reta, e é dado por:
Sendo assim, precisaremos derivar aqui.
Passo 2
Pra começarmos a nossa resolução, precisamos achar o valor de no ponto dado, pois como estamos trabalhando em uma parametrização em relação a , precisamos encontrar o valor de quando
Sabemos que
Assim,
Portanto, queremos tal que
Como só a primeira volta no circula trigonométrico é necessária, temos que
Passo 3
Para achar a inclinação, temos que derivar a curva:
Substituindo , achamos o coeficiente angular da reta tangente no ponto em que queremos:
Passo 4
Sabemos que a equação da reta tangente é
Assim,
Logo,
Portanto,
Então temos a nossa reta tangente. Para conferir se estamos certos, vou plotar o gráfico abaixo:
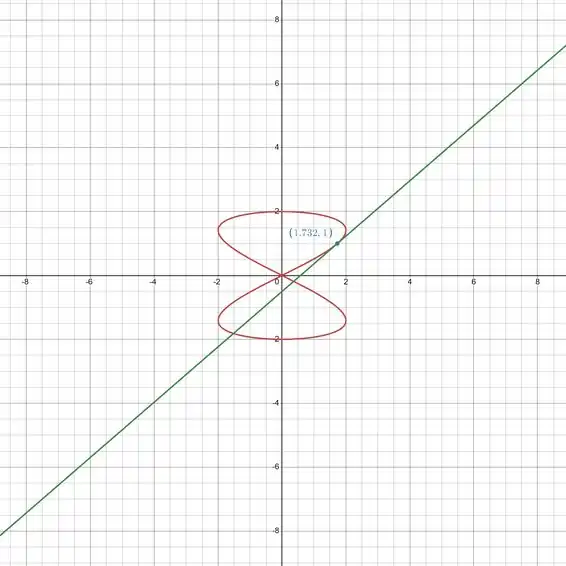
Veja que estamos corretos em relação ao que fizemos, temos a nossa reta em verde que é tangente no ponto em que precisamos.