Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 21
Descreve o movimento de uma partícula com posição ) quando varia no intervalo dado.
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade hoje.
O problema fornece as coordenadas e se uma partícula como função do tempo:
E devemos descrever qual o movimento de uma partícula que segue essa equação que descreve o seu movimento, dentro do intervalo
O que a gente vai fazer aqui para conseguir descrever o que acontece, é colocar a equação parametrizada em coordenadas cartesianas, a partir disso poderemos observar se obtemos uma equação de uma curva conhecida, como elipses, circunferências, parábolas, etc.
Para essa questão, o que vamos fazer para realizar essa transformação entre coordenadas é utilizar da identidade trigonométrica fundamental.
Passo 2
Assim, reescrevendo de forma a isolar o seno e o cosseno:
Da equação fundamental:
Trata-se de uma elipse com eixo maior na direção !
Veja que podemos facilmente encontrar quais os pontos que a figura encontra com os eixos:
Então nesses pontos a nossa figura encontra o eixo , agora vamos fazer o mesmo para o eixo :
Então nesses pontos a nossa figura encontra o eixo
Passo 3
Um esboço da trajetória é dado a seguir:
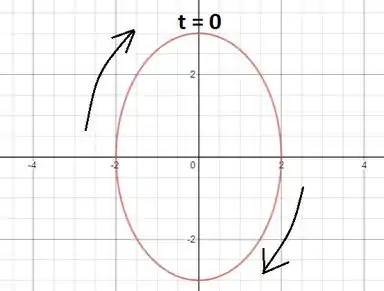
A partícula parte de quando e da uma volta completa no sentido horário, até o ponto .