Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 44
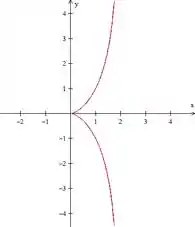
Encontre as equações paramétricas para o conjunto de todos os pontos , como mostrado na figura, tais que . Esboce a curva. (Essa curva é chamada cissoide de Diocles, em homenagem ao estudioso grego Diocles, que introduziu a cissoide como um método gráfico para a construção da aresta de um cubo cujo volume é o dobro daquele de um cubo dado).
Passo 1
Queremos encontrar as coordenadas do ponto m função de .
Vamos considerar um triângulo inscrito na semicircunferência, e um outro trângulo dentro dele, assim:
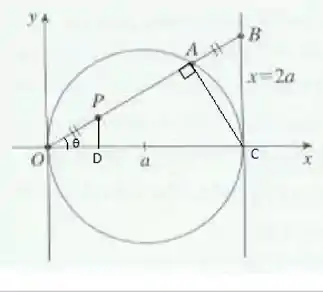
Todos são triangulos retângulo.
Podemos dizer que as coordenadas de são
Tranquilo? Tirei isso de relações trigonométricas do triangulo
Agora precisamos descobrir quanto vale . E vamos fazer isso descobrindo quanto vale , já que eles são iguais.
Passo 2
Para isso, vamos usar o triangulo
Podemos dizer que
Assim
Agora, pelo triangulo grandão , podemos dizer que:
Opa, temos e temos . Com isso, podemos achar e consequentemente pois
Passo 3
Assim, a parametrização da nossa curva fica:
Passo 4
Esboçando a curva, arbitrando e chutando alguns valores para temos:
Resposta
