Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 43
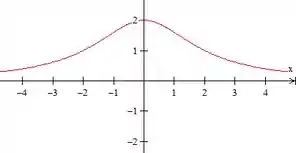
Uma curva, denominada bruxa de Maria Agnesi, consiste em todas as possíveis posições possíveis do ponto na figura. Mostre que as equações paramétricas para essa curva podem ser escritas como
Esboce a curva.
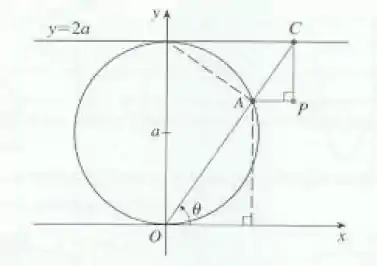
Passo 1
Queremos as coordenadas do ponto em função de , certo?
Vamos imaginar alguns triângulos retângulos nessa figura, assim:
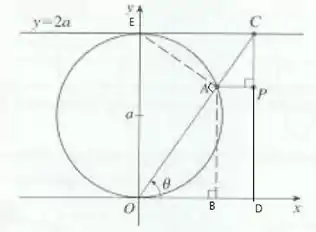
Então temos o triângulo menorzinho, que é o triângulo , o triangulo maior, que é o triangulo , temos também o triângulo e, por fim, o triangulo , que está inscrito na semi circunferência, beleza?
E ah, importante! Como esse ultimo triangulo tá inscrito na semi circunferência,ele também é triângulo retângulo, tá certo?
Se você reparar pela figura podemos dizer que as coordenadas do nosso ponto são
Só precisamos descobrir a medida desses segmentos e teremos a parametrização que queremos.
Passo 2
Como estamos falando de triângulos retângulos, podemos usar relações com seno e cosseno, assim:
Do triangulo :
OK, vamos reservar isso.
E do triangulo :
Reservamos isso também.
Passo 3
O que sabemos até agora é que
Agora vamos descobrir a medida desses segmentos e e matar logo essa questão.
Vamos primeiro descobrir
Pra isso, vamos olhar pro triangulo que tá inscrito na semi circunferência, o triangulo .
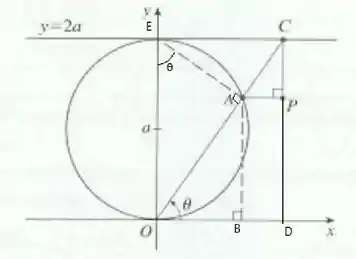
Olhando para esse triangulo, temos que
Lembrando que é um algulo alterno interno.
Assim,
Já provamos uma parte!
Falta só provar a parametrização do agora.
Passo 4
Vamos lá.
Precisamos descobrir quando vale o segmento .
Para isso vamos olhar o triangulo maior, .
O segmento vale , assim, podemo dizer que
Substituindo em :
E nada mais é do que a tal da cotangente. Assim,
Passo 5
Fazendo , e escolhendo alguns valores de dentro do intervalo , o esboço da curva fica
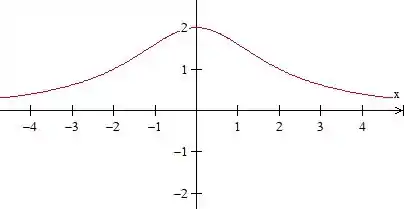
Resposta
