Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.5 - Ex. 27
Para quais valores de é válido que e ?
Passo 1
Fala galera, tudo bem? Essa questão parece complicad,a mas vou te ajudar! Temos essa inequação
E o problema quer saber para quais valores satisfaz essa relação! Ainda temos o limite de validade de
A ideia é usar uma calculadora gráfica e fazer o gráfico tanto de
Quanto de
Assim vamos poder verificar onde a função módulo é menor do que ! É uma solução bem gráfica e muito poderosa!
Mas relaxa, vou fazer com você!
Passo 2
Podemos traçar dois gráficos utilizando uma calculadora gráfica e verificar os pontos em que essas funções se interceptam. Nossas funções são
e a reta horizontal
sendo limitado por .
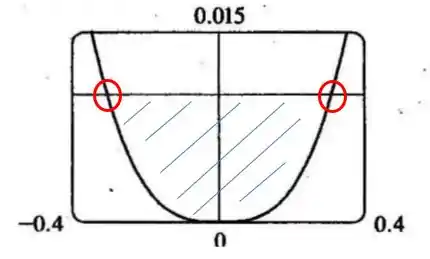
Note que a função módulo está completamente acima do eixo . Temos dois pontos onde as curvas se encontram: essas são as soluções para nossa equação, se trocassemos o sinal de maior pelo de igualdade
Esses pontos estão circulados em vermelho. Mas não queremos a igualdade, queremos o intervalo em que
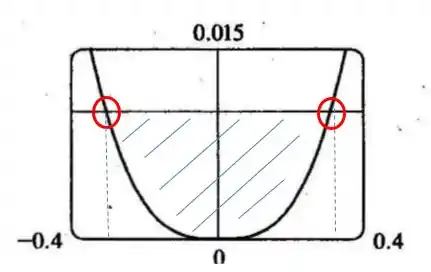
Entçao queremos abaixo da reta horizontal, sendo assim o intervalo está representado em azul e delimitado pelas retas pontilhadas verticais azuis
Passo 3
As coordenadas x desses pontos de interseções (que são as soluções das equações) são aproximadamente .
Logo, para a condição de vale qualquer entre os valores que é a região sombreada.
Beleza? Espero ter ajudado!