Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.5 - Ex. 28
Encontre uma formula explicita para e use-a para fazer na mesma tela um gráfico , e da reta . Para verificar seu trabalho, veja se os gráficos de e são reflexões em torno da reta.
Passo 1
Belezinha, pessoal. O enunciado da questão pede pra encontrarmos a inversa dessa função aqui:
Pra fazermos isso, precisamos encontrar uma maneira de escrever como uma função de . Isso significa que precisamos isolar o .
Vamos ver direitinho como fazer isso.
Passo 2
Vamos lá! Pra facilitar um pouco a vida, vamos escrever no lugar de :
Vamos que o aparece apenas uma vez em toda a expressão, então vamos tentar isolar esse termo diretamente:
E agora? Como fazemos pra retirar aquele do expoente? Basta aplicarmos logaritmo dos dois lados da equação:
Por fim, temos que:
Pra fechar, vamos só chamar de e de :
Passo 3
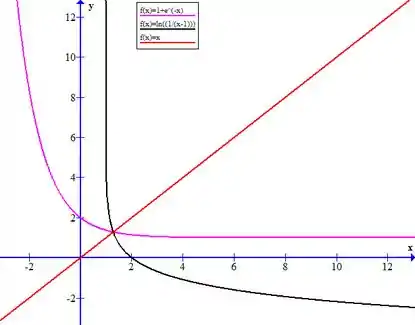
Agora, só precisamos usar uma calculadora gráfica pra traçamos o gráfico da função dada, da inversa que encontramos e da reta .
Olha só como fica:
