Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.4 - Ex. 26
Compare as funções e através do gráfico de ambas as funções. Encontre todos os pontos de interseção dos gráficos corrigidos a uma casa decimal. Qual função cresce mais rapidamente quando é grande?
Passo 1
Eaee, belezinha?? Bom...queremos comparar as seguintes funções através de seus gráficos:
Com isso, queremos encontrar todos os pontos de interseção dos gráficos corrigidos a uma casa decimal.
Com essa plotagem, poderemos verificar qual função cresce mais rapidamente quando é grande.
Mas o que quer dizer com “crescer mais rapidamente”??
Bom... quando uma função cresce mais rapidamente do que outra, isso significa que, à medida que você aumenta os valores de entrada (por exemplo, em ), a função que cresce mais rapidamente aumenta seus valores de saída (ou seja, ) a uma taxa maior do que a outra função.
Passo 2
Bom pessoal, os pontos de interseção dos gráficos podem ser encontrados por:
Já dá para perceber que uma solução imediata é , pois fazendo , temos:
Nesse ponto de interseção. Temos que é:
Logo, o ponto de interseção é .
Masss, o enunciado pediu para plotarmos os gráficos e verificarmos todos os pontos de interseção.
Utilizando uma Software matemático, temos:
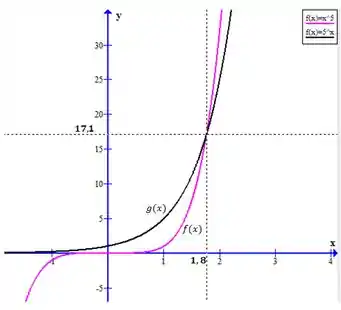
Logo, temos outro ponto de interseção:
Mas queremos saber qual função cresce mais rapidamente quando é um valor grande.
Passo 3
Para pequenos valores de , temos o seguinte comportamento: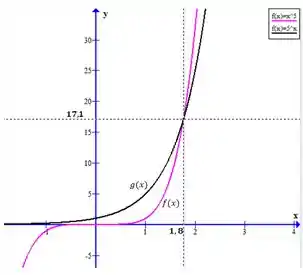 
Nesse caso, a função cresce de forma mais rápida.
Mas ainda temos um outro ponto de interseção (o ponto ), onde o comportamento irá mudar.
Passo 4
Mas para grandes valores de , temos comportamento abaixo:
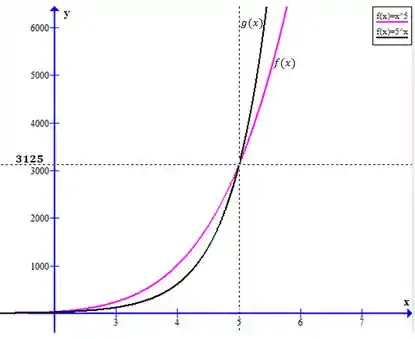
O gráfico foi dividido pelo fato de a escala estar muito diferente para as duas interseções.
Desta forma, fica mais fácil visualizar.
Para grandes valores de , vemos que .
Assim, cresce de forma mais rápida!!
Resposta
cresce de forma mais rápida para grandes valores de .