Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 14

Encontre pelo menos 10 somas parciais da série. Transforme em gráfico a sequência dos termos e a sequência das somas parciais no mesmo desenho. A série é convergente ou divergente? Se é convergente, encontre a soma. Se for divergente, explique o porquê.

∑ n = 1 ∞ s e n 1 n - s e n 1 n + 1

Passo 1

Fala, pessoal! Tudo tranquilo?

Bom, vamos começar entendendo o que precisaremos fazer nesse caso:

A questão pede primeiro para encontrarmos 10 somas parciais da série.

Depois, plotaremos em um gráfico tanto a sequência dos termos quanto das somas parciais.

Daí vamos precisar entender se a série é convergente ou divergente e para isso basta calcular o limite da sequência.

Vamos lá!

Passo 2

Vamos chamar de a n o termo dentro do somatório, beleza? Assim, temos:

a n = s e n 1 n - s e n 1 n + 1

Nos foi pedido pra calcular os 10 primeiros termos desse somatório. Mãos a obra!

s 1 = a 1 = s e n 1 1 - s e n 1 1 + 1 ≈ 0,3620

s 2 = s 1 + a 2 = 0,3620 + s e n 1 2 - s e n 1 2 + 1 = 0,5142

s 3 = s 2 + a 3 = 0,5142 + s e n 1 3 - s e n 1 3 + 1 = 0,5940

s 4 = s 3 + a 4 = 0,5940 + s e n 1 4 - s e n 1 4 + 1 ≈ 0,6428

s 5 = s 4 + a 5 = 0,6428 + s e n 1 5 - s e n 1 5 + 1 ≈ 0,6755

Metade do caminho! Vamo que vamo:

s 6 = s 5 + a 6 = 0,6755 + s e n 1 6 - s e n 1 6 + 1 ≈ 0,6990

s 7 = s 6 + a 7 = 0,6990 + s e n 1 7 - s e n 1 7 + 1 ≈ 0,7167

s 8 = s 7 + a 8 = 0,7167 + s e n 1 8 - s e n 1 8 + 1 ≈ 0,7305

s 9 = s 8 + a 9 = 0,7305 + s e n 1 9 - s e n 1 9 + 1 ≈ 0,7416

s 10 = s 9 + a 10 = 0,7416 + s e n 1 10 - s e n 1 10 + 1 ≈ 0,7506

Passo 3

Nosso gráfico terá duas sequências, uma dos termos s n , ou seja, os termos da soma, tanto dos termos a n , ou seja, termos da sequência

Vamos olhar agora para o gráfico da série e dos termos!

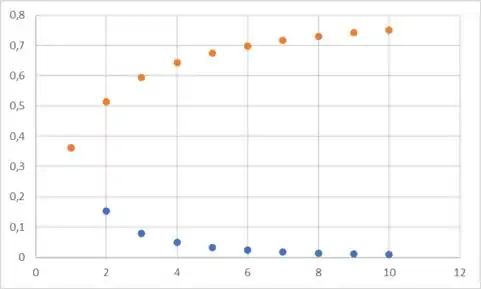
Os pontos azuis representam os termos da sequência e os laranjas as somas parciais.

Pelo comportamento dos pontos azuis já podemos ter uma ideia de que a série vai convergindo para algum valor, então vamos calcular nosso limite para descobrirmos qual é.

Veja que a sequência tende a zero, o que reforça nossa hipótese de convergência da série.

Passo 4

Para descobrirmos para que valor a série converge, vamos resolver o limite da sequência das somas parciais, mas para isso precisamos escrever essa sequência expandindo o somatório.

Para isso subtituimos nossas incógnitas n por 1,2,3,4,5,..., n - 1 , n .

Se expandirmos o somatório teremos:

∑ n = 1 N s e n 1 n - s e n 1 n + 1 =

= s e n 1 1 - s e n 1 2 + s e n 1 2 - s e n 1 3 + … +

s e n 1 N - 1 - s e n 1 N + s e n 1 N - s e n 1 N + 1

Temos aqui que todos os termos vão se cancelar pois tem mesmo valor com sinais opostos, com excessão do primeiro e do último termo restando apenas:

s e n 1 - s e n 1 N + 1

Passo 5

Agora que já temos nosso s n simplificado, vamos voltar com esse resultado para o limite:

lim N → ∞ ⁡ s e n 1 - s e n 1 N + 1 = s e n ( 1 ) - s e n ( 0 ) = s e n ( 1 )

Assim, podemos dizer que a série é convergente e converge para s e n ( 1 ) .

Resposta

A série é convergente!

lim N → ∞ ⁡ ∑ n = 1 N s e n 1 n - s e n 1 n + 1 = s e n ( 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada um dos Exercícios 1-6 dá uma fórmula para o n-ésimo termo a n de uma sequência {a n}. Encontre os valores de a1 , a2 , a3 e a4 .
Cada um dos Exercícios 1-6 dá uma fórmula para o n-ésimo termo a n de uma sequência {a n}. Encontre os valores de a1 , a2 , a3 e a4 .
Cada um dos Exercícios 1-6 dá uma fórmula para o n-ésimo termo a n de uma sequência {a n}. Encontre os valores de a1 , a2 , a3 e a4 .
Cada um dos Exercícios 7-12 dá um ou dois termos iniciais de uma sequência, bem como uma fórmula de recursão para os termos remanescentes. Escreva os dez termos iniciais da sequência.
Cada um dos Exercícios 7-12 dá um ou dois termos iniciais de uma sequência, bem como uma fórmula de recursão para os termos remanescentes. Escreva os dez termos iniciais da sequência.