Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 4
Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico.
Passo 1
Eaee, belezinha??? Bom... o enunciado nos dá a seguinte equação de uma parábola:
Queremos encontrar o vértice, o foco e sua diretriz.
Mas antes de definirmos, vamos colocar nossa equação assim:
Temos partir da definição de parábola que:
Esse parâmetro é que nos vai dizer onde está o vértice, o foco e a diretriz.
O parâmetro é a distância entre o vértice da parábola e o foco ao longo do eixo .
Se a parábola está voltada para cima ou para baixo, o foco está localizado em , e se a parábola está voltada para a esquerda ou para a direita, o foco está localizado em .
E a diretriz??
Se a parábola está voltada para cima ou para baixo (isto é, na forma ), a diretriz é uma reta horizontal localizada a uma distância abaixo do vértice.
Se a parábola está voltada para a direita ou para a esquerda (ou seja, na forma ), a diretriz é uma reta vertical localizada a uma distância à esquerda do vértice.
Por fim, basta plotarmos a curva!! 😉
Passo 2
Analisando a expressão , de acordo com o que acabamos de ver no passo , podemos concluir que a nossa parábola tem concavidade voltada para baixo.
Como sabemos disso?? Assim:
- O termo indica que a parábola é simétrica em relação ao eixo , o que significa que ela pode ser aberta para cima ou para baixo, dependendo do sinal do coeficiente de .
- O termo tem um coeficiente negativo , o que indica que a parábola está se movendo para abaixo ao longo do eixo .
Assim, comparando as duas expressões temos que
Logo, pelo que vimos no Passo 1, podemos constatar que:
- O vértice da parábola se encontra na origem;
- seu foco é dado por ;
- e sua diretriz é .
Passo 3
A partir dos dados encontrados nos passos anteriores, podemos esboçar a seguinte parábola:
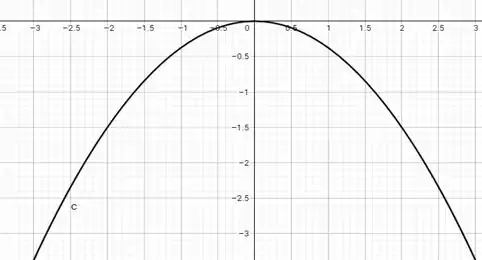
Resposta
O vértice da parábola se encontra na origem, seu foco é dado por e sua diretriz é .
