Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 11
Encontre os vértices e os focos da elipse e esboce seu gráfico.
Passo 1
A elipse dada é:
A equação geral é:
O foco da elipse é encontrado em:
O a gente acha fazendo:
Já o vértice é encontrando em:
E para a gente encontrar esses valores de e a gente precisa é comparar as equações.
Passo 2
Comparando as expressões, temos que:
A distância focal é dada pelo parâmetro c, definido por:
Passo 3
Dessa forma, podemos concluir que a elipse dada possui centro na origem, com vértices em . Os focos são .
Vamos utilizar o GeoGebra para gerar esse gráfico:
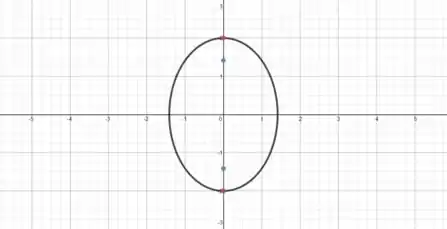
Em vermelho a gente tem os vértices, e em azul a gente tem os focos.
Resposta
A elipse dada possui centro na origem, com vértices em . Os focos são .
Exercícios de Livros Relacionados
Desenhe um esboço do gráfico da equação: x * y = 9
Desenhe um esboço do gráfico da equação: x = y^2 + 2
Desenhe um esboço do gráfico da equação: x = y^2 - 4
Desenhe um esboço do gráfico da equação: x + 3 * y = 0
Desenhe um esboço do gráfico da equação: x^2 - 9 * y^2 = 0