Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 25
Encontre a área da região que está dentro da primeira curva e fora da segunda curva:
Passo 1
Oiii, tudo certinho?? Bom... o enunciado nos dá duas equações polares:
E
Queremos calcular a área que está dentro da primeira curva e fora da segunda curva.
Em outras palavras, para ficar melhor de saber o que vamos calcular, queremos encontrar a seguinte área hachurada:
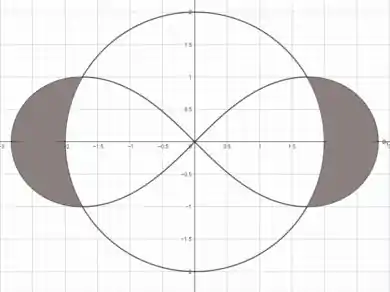
Para isso, sabemos que, quando estamos trabalhando em coordenadas polares, a área é dada pela seguinte integral:
Assim, devemos encontrar a interseção entre as curvas para aplicar na integral, juntamente com os limites de integração que iremos encontrar.
Agora bora lá!! 😉
Passo 2
Na interseção entre as curvas, igualamos as funções:
Podemos ver através do passo 1 que a área da seção procurada é vezes a área da seção compreendida entre as curvas de a , dessa forma, nossos limites de integração são e.
Passo 3
Para calcular a área abaixo de uma curva, lembramos que:
Note que já multiplicamos por de acordo com o que vimos no passo anteior.
Substituindo os limites de integração e aplicando a subtração das funções (já que queremos a área de interseção entre as duas), temos:
Passo 4
Podemos separar em 2 integrais:
Na primeira integral, podemos fazer por substituição simples. Seja
Assim podemos reescrever a integral como:
Voltando para a variável original temos:
A segunda integral é dada por:
Assim, a área procurada é a subtração dessas 2 integrais, ou seja:
Resposta
A área da seção é .