Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 8
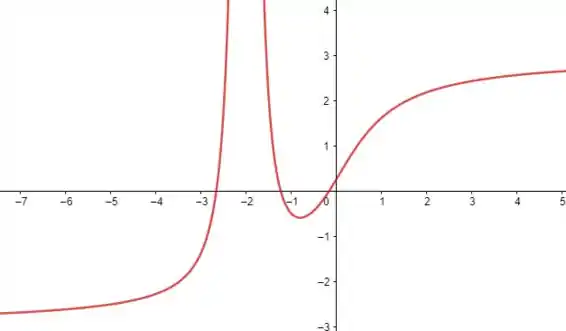
Esboce o gráfico de um exemplo de uma função que satisfaça todas as condições dadas
Passo 1
Olá, querido estudante. Vou te ajudar a resolver mais uma atividade.
Aqui a gente precisa esboçar o gráfico de uma função qualquer, desde que ela satisfaça as seguintes condições:
Isso quer dizer que, ao nos aproximarmos de nossa função deverá ‘explodir’ para valores extremamente grandes e positivos.
Quando estivermos caminhando ao longo do eixo para valores cada vez menores, nossa função irá cada vez mais se aproximar de e por último, quando estivermos caminhando ao longo de eixo para valores cada vez maiores, nossa função irá cada vez mais se aproximar de .
Não precisamos pensar em cada equação que irá compor os intervalos da nossa função, apenas o gráfico.
Passo 2
Precisamos então que:
- a medida que nos aproximamos de a funções irá crescer indefinidamente;
- a medida que caminhe no eixo a função se aproxime de ;
- a medida que caminho no eixo a função se aproxime de .
Um gráfico dos vários possíveis, é o seguinte:
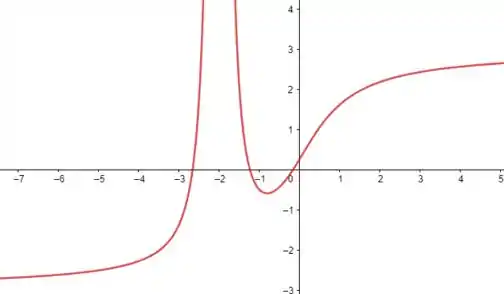
Resposta
