Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as curvas:
Temos em mãos duas funções trigonométricas no intervalo de:
A primeira coisa que temos que fazer é esboçar o gráfico! As nossas funções são funções trigonométricas bem conhecidas, então não tem mistério!
Para o nosso intervalo temos:
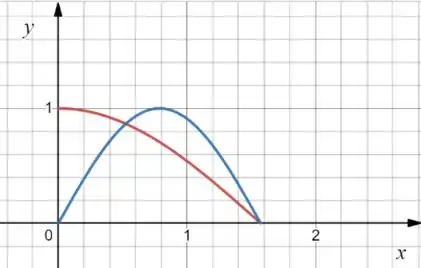
Onde é a curva vermelha e é a curva azul!
Passo 2
Fazendo a interseção das equações temos:
Se , temos:
Simplificando...
A partir dessa equação tiramos que:
Esse será o nosso intervalo de integração. Que é essa areazinha verde:
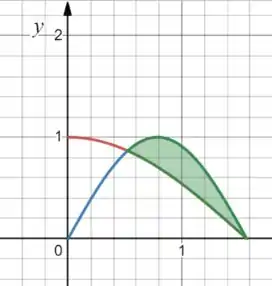
Com isso temos duas regiões: a primeira de até e a segunda de até .
Agora podemos calcular a área!!
Passo 3
Temos a seguinte integral:
Resolvendo a primeira integral:
Resolvendo a segunda integral:
Prontinho! Agora é só juntar as duas respostas:
É isso! Entendeu tudo? Responde Aí!