Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 64
Estime os intervalos da concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de .
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá para gente a função:
E pede pra gente estimar os intervalos da concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de .
Então aqui o lance é o seguinte. Nós vamos fazer o cálculo da derivada da função e plotar o gráfico dessa derivada. E depois vamos analisar com calma esse gráfico para encontrar os intervalos de concavidade.
Para isso precisamos lembrar que a concavidade pode ser avaliada de acordo com o sinal da segunda derivada da função. Sendo
Ou seja, com o gráfico de em mãos, basta olhar a inclinação de suas retas tangentes, pois elas são so valores de e seguir essa descrição acima.
Partiu ver isso acontecendo!!!
Passo 2
Por meio de uma ferramenta gráfica, temos o seguinte gráfico de (a derivada de ):
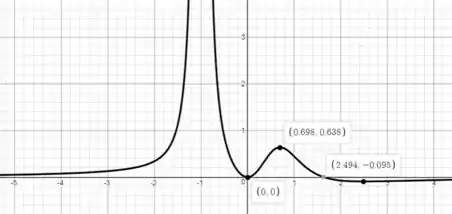
Se a derivada de uma função indica o decrescimento e decrescimento dessa função então sabemos que (a derivada de ) é positiva para os intervalos onde é crescente e negativa para os intervalos onde é decrescente então:
se ou ou
e
se ou .
Passo 3
Se
possui concavidade voltada para cima para valores de aproximadamente nos intervalos , e e concavidade para baixo no intervalo e .
Resposta
possui concavidade voltada para cima para valores de aproximadamente nos intervalos , e e concavidade para baixo no intervalo e .