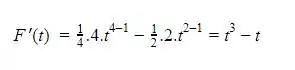Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.3 - Ex. 9
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.
9.
Passo 1
Neste tipo de questão não tem muito o que se retirar do enunciado, basta utilizar as fórmulas existentes ao longo da seção para derivada de diferentes tipos de função. Pois, o processo de cálculo da derivada de uma função , a partir da Definição, em geral é lento, então utiliza-se desses artifícios para nos auxiliar no cálculo de derivadas e acelerar o processo de resolução de problemas deste tipo.
Passo 2
Assim , a derivada da função em questão será dada por
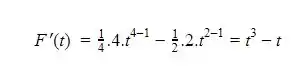
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.12. G y = y 10 + 7 y 5 - y 3 + 1
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.7. f x = 1 8 x 8 - x 4
2.Considere um objeto movendo-se com uma função posição s = f ( t ) .( a ) Escreva uma expressão para a velocidade média no intervalo de tempo desde t = a até t = a + h ( b ) Escreva uma expressão par
23 . ( a ) Use os dados do Exemplo 5 para achar a taxa média da mudança da temperatura em relação ao tempo. ( i ) das 8 horas da noite às 11 horas da noite. ( i i ) das 8 horas da noite às 10 horas da
20. O deslocamento (em metros) de uma partícula movendo-se ao longo da reta é dado pela equação s = t 2 - 8 t + 18 , onde t é medido em segundos. ( a ) Encontre as velocidades médias sobre os seguinte