Para os Exercícios 51-54 encontre o ângulo , onde .
52.
Passo 1
Se tirarmos a raiz quadrada dos dois lados da equação chegamos direto na resposta:
Existem 4 valores em que isso acontece, e :
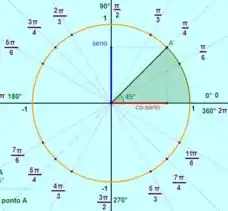
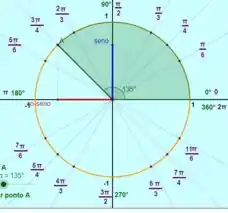
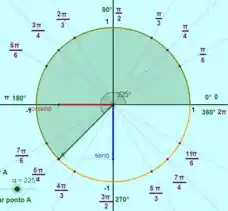
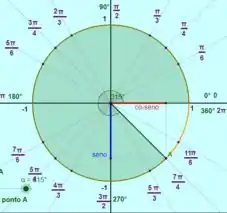
Para os Exercícios 51-54 encontre o ângulo , onde .
52.
Se tirarmos a raiz quadrada dos dois lados da equação chegamos direto na resposta:
Existem 4 valores em que isso acontece, e :



