Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.8 - Ex. 4
Nos exercícios 1 a 8, (a) ache a excentricidade, os focos e as diretrizes da cônica central dada.(b) Faça um esboço mostrando a cônica, os focos e as diretrizes. Também escolha quatro pontos P ( um em cada quadrante) sobre a cônica e trace os segmentos de reta cujos comprimentos são as distâncias não orientadas de P ao foco e à diretriz correspondente. Observe que a razão entre essas distâncias é
Passo 1
Para encontra o que está sendo pedido na letra (a) basta seguir os passos mostrados ao longo da seção quando estamos trabalhando com as cônicas. Ao longo da seção tem um exemplo bem explicativo que será tomado como base para resolução das questões que se seguem.
Passo 2
Letra (a)
Da equação da elipse dada, e . , assim temos que . Logo, de (16), . Como , segue do Teorema 10.8.2 que a diretriz correspondente ao foco em ( ) tem equação , e a diretriz correspondente ao foco em ( ) tem equação .
Passo 3
Letra (b)
Um esboço do gráfico mostrando a cônica , os focos e os 4 pontos pedidos pode ser representado da seguinte forma :
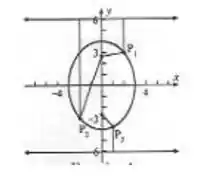
Resposta
Letra (a)
.
( ) e ( )
e
Letra (b)
Gráfico.