Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.7 - Ex. 22

Nos Exercícios 17-24, encontre a excentricidade da hipérbole. Em seguida, encontre e desenhe os focos e diretrizes da hipérbole.

y 2 - 3 x 2 = 3

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

Primeiramente, nosso objetivo será reescrever a equação da hipérbole dada na sua forma reduzida, que tem o seguinte formato:

x 2 a 2 - y 2 b 2 = 1

A partir disso, teremos as medidas dos a e b , e poderemos obter, pelo Teorema de Pitágoras, a medida do foco c . Para, enfim, determinarmos a excentricidade, os focos e as diretrizes da hipérbole.

Cumprindo isso, poderemos traçar o gráfico, com auxílio de um software, destacando os pontos relevantes da hipérbole.

Simbora?

Passo 2

Pegando a equação dada, vamos simplifica-la, dividindo todos termos por 3:

y 2 - 3 x 2 = 3

y 2 3 - x 2 1   =   1

Assim, temos,

a 2   =   3 ;   b 2   = 1

Lembrando que entre os denominadores, o valor de a é sempre o do eixo maior.

Como, por Pitágoras:

c =   a 2 + b 2  

Então,

c =   3 + 1 = 4 = 2

Sendo assim, a excentricidade da hipérbole é:

e = c a = 2 3 = 2 3 3  

Os focos da hipérbole são dados por F ( 0 , ± c ) , logo:

F 1 0 , 2   e   F 2 ( 0 , - 2 )

Já as diretrizes da hipérbole são dadas por y = ± a e , logo:

y = ± 3 2 3 3 = ± 3 2

Passo 3

Traçando o gráfico da hipérbole, temos:

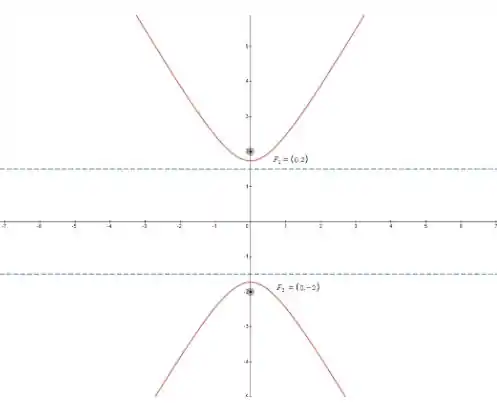
Onde os pontos em preto são os focos e as linhas em azul são as diretrizes.

Espero ter ajudado! Abraços e até a próxima!

Resposta

Excentricidade: e = 2 3 3 . Foco: ( 0 , ± 2 ) . Diretrizes: x = ± 3 2 .

Exercícios de Livros Relacionados

Os Exercícios 25-28 fornecem as excentricidades e os focos ou focos das hipérboles centradas na origem do plano xy. Em cada um dos casos, encontre a equação de forma padrão da hipérbole nas coordenada
Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 169 x 2 +25 y 2 =4225
Nos Exercícios 17-24, encontre a excentricidade da hipérbole. Em seguida, encontre e desenhe os focos e diretrizes da hipérbole. y 2 - x 2 = 4
Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 2 x ²+y ²=4 ² ²
Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 9 x ²+10 y ²=90 ² ²