Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.7 - Ex. 40
Esboce as parábolas e elipses nos Exercícios 37-44. Inclua a diretriz correspondente ao foco na origem. Rotule os vértices com coordenadas polares apropriadas. Rotule também os centros das elipses.
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
Neste problema, nosso objetivo será, através da equação polar dada, identificar se a cônica dada é uma parábola ou elipse, determinar qual a sua diretriz e esboçar um belo gráfico contendo a curva, seus vértices e diretriz(es).
Simbora?
Passo 2
Veja que a equação dada, tem o seguinte formato:
Basta dividirmos todos os termos por 2, e reescrevendo da seguinte forma:
Comparando as equações, obtemos:
Ainda observando a equação, identificamos o sinal negativo no denominador e a função cosseno o que significa que a diretriz é na direção vertical e pode ser descrita por .
Temos, assim:
Excentricidade: o que indica uma parábola.
Diretriz:
Veja ainda, que para , temos:
Portanto o vértice é: .
Passo 3
Agora, traçando a cônica com auxílio de um software e destacando as informações pedidas, obtemos:
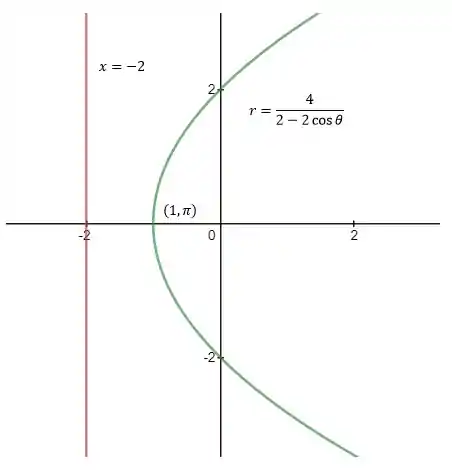
Espero ter ajudado! Abraços e até a próxima!
Resposta
Excentricidade: . Diretriz: . Vértice: .