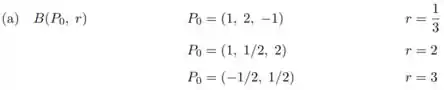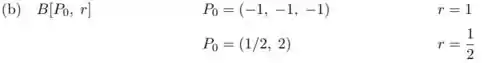Exercícios de Elipsóide, Esfera e Hiperbolóides - Lista de Exercícios Resolvida
Questão 2
Seja a quádrica cuja equação cartesiana é dada por .
Identifique a quádrica.
Ver solução completaQuestão 3
Considere a superfície em dada pela equação .
Identifique a superfície quádrica e desenhe a figura correspondente a essa quádrica.
Ver solução completaQuestão 5
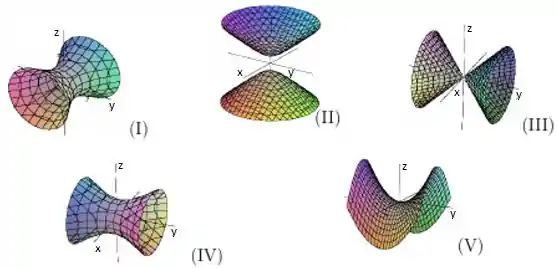
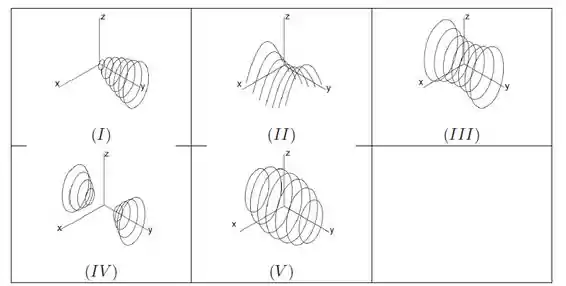
Associe cada quádrica ao gráfico que mais se assemelha a ela:
i) 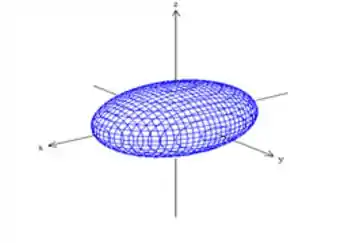
ii) 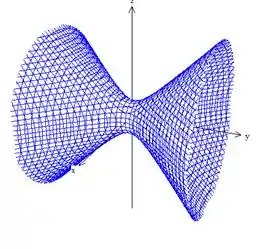
iii) 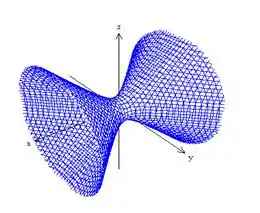
iv) 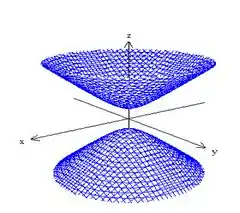
v) 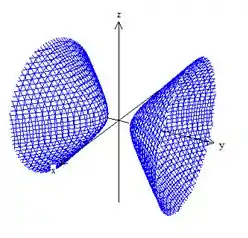
Questão 6
Seja a quádrica cuja equação cartesiana é dada por .
Identifique a quádrica.
Ver solução completaQuestão 7
Seja a superfície dada por
E considere as seguintes afirmações:
- é um hiperboloide de uma folha
- A interseção entre e o plano é uma parábola neste plano
- A interseção entre e o plano é vazia
Indique a alternativa correta.
- Todas as afirmações são falsas
- Todas as afirmações são verdadeiras
- As afirmações II e III são verdadeiras e I é falsa
- As afirmações I e III são verdadeiras e a II é falsa
- A afirmação II é verdadeira e I e III são falsas
Questão 8
Considere a função
Seja a superfície de nível de passando pelo ponto e seja a superfície dada pela equação
Dentre as superfícies, temos:
- Um cone com vértice no ponto
- Dois planos contendo o eixo e um elipsóide centrado no ponto
- Um parabolóide hiperbólico
- Um cilindro e uma esfera centrada no ponto
- Um hiperbolóide de duas folhas
Questão 9
A interseção entre o cilindro , a esfera e o semi espaço é:
- Uma circunferência em um plano paralelo ao plano
- Uma circunferência em um plano paralelo ao plano
- Uma elipse em um plano paralelo ao plano
- Duas elipses, cada uma em um plano paralelo ao plano
- Duas circunferências, cada uma em um plano paralelo ao plano
Questão 11
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(b)
Ver solução completaQuestão 12
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(a)
Ver solução completaQuestão 13
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(c)
Ver solução completaQuestão 15
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(e)
Ver solução completaQuestão 16
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(f)
Ver solução completaQuestão 17
Determine a equação de uma elipsoide que passe pelo ponto e intersecte o plano na elipse
Ver solução completaQuestão 18
2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(d)
Ver solução completaQuestão 19
(Capítulo 15.8 – Exercício 8) Identifique a superfície cuja equação é dada.
Ver solução completaQuestão 20
2.4. Mostre que o elipsoide e a esfera se tangenciam no ponto (isto é, que elas têm o mesmo plano tangente neste ponto).
Ver solução completaQuestão 25
As interseções da superfície definida por com planos paralelos ao plano estão representados na figura a seguir:
a)Nenhuma das alternativas
b)
c)
d)
e)
f)
Ver solução completa