Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 30

Os Exercícios 27-34 fornecem equações para hipérboles. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu esboço.

y 2 - x 2 = 4

Passo 1

Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Primeiro, temos a equação da hipérbole dado por:

y 2 - x 2 = 4

Dessa forma, para a forma padrão:

x 2 a 2 - y 2 b 2 = 1

Simplificamos tudo por 8. Logo, concluímos que a forma padrão é:

- x 2 4 + y 2 4 = 1

Portanto, a forma os parâmetros são:

a = 2

b = 2

Dessa forma, para o foco:

c = a 2 + b 2 = 4 + 4 = 8

Passo 2

Para as assíntotas, da equação:

y 2 - x 2 = 4

Procedemos:

y 2 - x 2 = 0

Logo,

y = ± x

Portanto, nosso esboço fica:

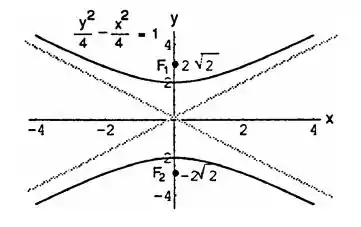
E é isso meus queridos, até a próxima!

Resposta

- x 2 4 + y 2 4 = 1

Exercícios de Livros Relacionados

Nos Exercícios 17-24, encontre a excentricidade da hipérbole. Em seguida, encontre e desenhe os focos e diretrizes da hipérbole. 64 x 2 - 36 y 2 = 2304
Os Exercícios 25-28 fornecem as excentricidades e os focos ou focos das hipérboles centradas na origem do plano xy. Em cada um dos casos, encontre a equação de forma padrão da hipérbole nas coordenada
Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 169 x 2 +25 y 2 =4225
Nos Exercícios 17-24, encontre a excentricidade da hipérbole. Em seguida, encontre e desenhe os focos e diretrizes da hipérbole. y 2 - x 2 = 4
Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 2 x ²+y ²=4 ² ²