Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 105
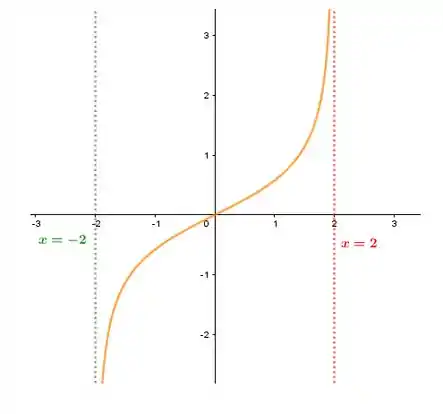
Faça o gráfico da função
Explique a relação entre a fórmula e o que você observa.
Passo 1
O primeiro passo é considerar e observar o que essa função tem a nos “dizer”.
Observe que o domínio de corresponde , pois qualquer valor fora desse intervalo ocasionaria em uma raiz quadrada negativa, que é algo que não existe no conjunto dos números Reais . Dessa maneira, veremos que o gráfico de estará “dentro” do intervalo (-2,2) .
Passo 2
O segundo passo é perceber que ao olharmos , veremos que estamos com uma divisão de polinômios, que tem alguns “probleminhas” quando ou , ou seja, quando substituímos esses números o denominador zera.
Passo 3
O terceiro passo é notar que quando isso acontece significa que possui assíntotas verticais. Porém, é necessário verificar se isso é verdade, ou seja, precisamos ver se, e .
No entanto, vimos que está definida somente para , sendo assim não podemos calcular e pois para estes pontos a função não está definida.
Dessa maneira, verificaremos apenas se e .
O que é simples de verificar pois só precisaremos substituir no limite à esquerda e ver o que acontece,
Da mesma forma, substituindo no limite à direita temos,
Isso é importante, pois é como se a função estivesse conversando conosco, e dizendo que quando ela se aproxima de pela esquerda, ela atinge valores cada vez mais altos.
Já quando ela se aproxima de pela direita ela atinge valores muito grande, só que com sinal de menos.
Com isso, possui uma assíntota vertical em e outra em .
Resposta
possui uma assíntota vertical em e outra em .
