Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 109
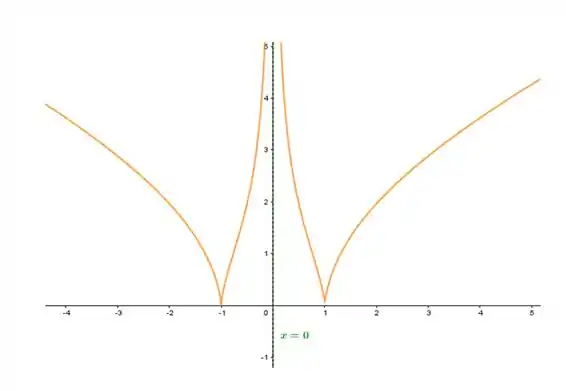
Faça o gráfico da função
Explique a relação entre a fórmula e o que você observa.
Passo 1
O primeiro passo é considerar e observar o que essa função tem a nos “dizer”.
Para isso precisamos reescrever . E isso pode ser feito calculando o MMC , ou seja,
Utilizando o famoso “quem tá no sol vai para sombra e quem está sombra vai para o sol” temos que , então
Sendo assim,
Passo 2
O segundo passo compreende ao item a, ou seja, teremos que observar o comportamento de quando . Para isso, utilizaremos a regra do produto (o limite do produto é o produto dos limites)
Substiuindo em teremos,
Sendo assim é uma assíntota vertical para .
Passo 3
O terceiro passo compreende ao item b, ou seja, observaremos o comportamento de quando . Para isso, dividiremos o numerador e o denominador pela maior potência de
Utilizando a regra do produto (o limite do produto é o produto dos limites),
Pela continuidade da função raíz cúbica podemos passar o limite para “dentro” da raíz,
Pela regra do quociente (o limite do quociente é o quociente dos limites) e a regra da subtração (o limite da subtração é a subtração dos limites).
Portanto, não possui assíntotas horizontais, já que
Passo 4
O quarto passo corresponde ao item c, ou seja, observaremos o comportamento de quando . Realizando primeiro o caso em que
Utilizando a regra do produto (o limite do produto é o produto dos limites)
Substituindo em teremos,
Utilizando as mesmas regras para o caso de teremos,
Sendo assim não é uma assíntota vertical para .
Resposta
Item a. Quando possui uma assíntota vertical .
Item b. Quando não possui assíntotas horizontais, já que
Item. Quando valores comuns ,ou, seja sem nenhuma particularidade.
