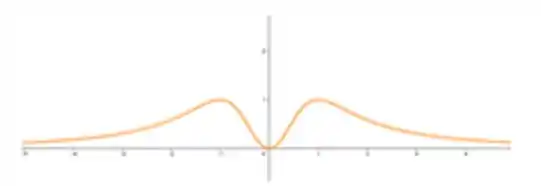
Faça o gráfico da função

Explique a relação entre a fórmula e o que você observa.

O segundo passo é olhar para e perceber que como se trata de uma função trigonométrica precisamos analisar as características do seu argumento,tais como: os valores máximos ou mínimos, se a é crescente ou não.

Dessa forma, Note que o argumento de é uma divisão da forma,

Onde não há nenhum número que possa zerar o denominador, sendo assim o domínio da função são todos os números Reais.

Outro fato interessante é perceber que o argumento de sempre será maior que zero e menor que Isso acontece, no primeiro caso está ao quadrado e consequentemente sempre será positivo, já e segundo caso , como o denominador é maior do que 1,então a fração será menor do que , ou seja,

Sendo assim, no intervalo de ,sabemos que é positiva,ou seja, seu gráfico está acima do eixo

Ale disso, outra coisa a ser analisada é para quais valores de , assume um máximo ou um mínimo . Com isso, percebemos que em ,

e,

Logo, assume seu máximo em .

Já , quando percebemos que

assume um mínimo.

O terceiro passo é observar o comportamento de quando , ou seja, estamos verificando se possui alguma assíntota horizontal.

Usando a continuidade da função seno podemos passar o limite para” dentro” o argumento de

Como é um número, então o argumento de é uma divisão de polinômios. Além disso como o limite é de , podemos dividir em cima e em baixo pela maior potência de , ou seja,

Utilizando a regra do quociente (o limite do quociente é o quociente dos limites) e a regra da soma (o limite da soma é a soma dos limites).

Portanto, quando se aproxima de zero, ou seja possui uma assíntota horizontal.