Faça o gráfico da função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas.
Passo 1
E aí, preparado para resolver mais essa questão sobre transformação de gráficos e funções? Bora lá!
Bom, essa questão pede pra gente desenhar o gráfico da função
sem fazer isso ponto a ponto.
Isso é, usaremos uma das funções básicas que estão na seção 1.2 do livro e aplicaremos as transformações necessárias para transformá-la nessa daí. Isso vai ajudar a gente a desenhar esse gráfico de maneira mais rápida e fácil.
Show de bola. Vamos ver quais são as características dessa função e qual a função básica que mais se parece com ela para fazer as mudanças adequadas. Vem que te ajudo com isso.
Passo 2
Temos que fazer o gráfico de:
Só que pra isso não podemos montar a tabelinha e marcar pontos, precisamos usar o gráfico de uma função já conhecida e aplicar transformações. Então, vamos olhar com calma para tudo que temos nessa função.
Repara que é uma função modular, e que dentro dela temos uma função de segundo grau.
Então vamos fazer as alterações aos poucos, ok?
Vamos começar com a função básica
O gráfico dela é uma parábola com concavidade voltada para cima. Assim:
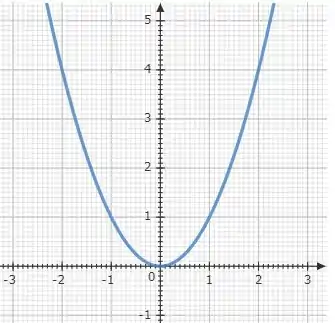
Mas nossa função é:
Então vamos fazer algumas transformações para desenhar seu gráfico corretamente.
Passo 3
Podemos começar transformando a função em um quadrado perfeito. Veja:
Que pode ser escrito com:
Agora a função se torna:
Que se parece com nossa função base, se fizermos
Teremos:
Que é a parábola deslocada uma unidade para baixo, já que estamos subtraindo em .
E nosso gráfico se torna:
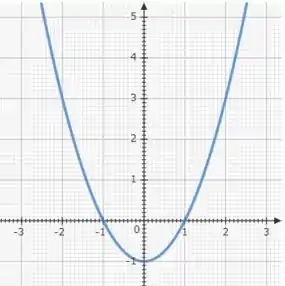
Passo 4
Além disso, nossa função também tem um deslocamento horizontal já que
e
Isso quer dizer que
E temos que deslocar nosso gráfico uma unidade para a direita. Assim:
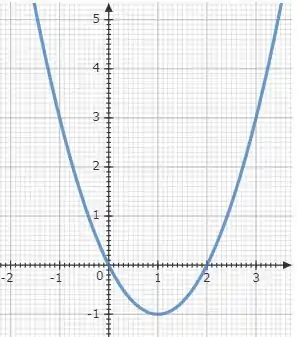
Show, já temos nosso gráfico quase pronto. Mas ainda precisamos lembrar que a função é modular.
Passo 5
O módulo fará com que nossa função tenha a parte abaixo do eixo seja refletida.
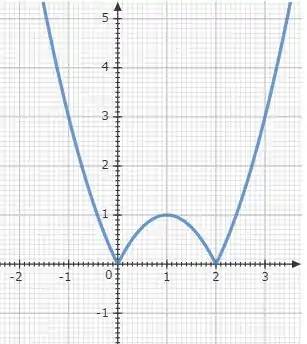
Esse processo nos dará o gráfico da função desejada:
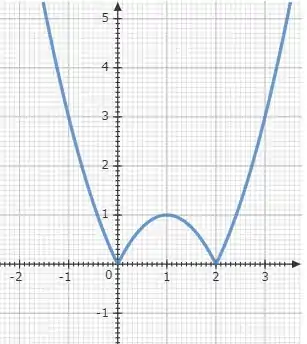
E prontinho. Gráfico plotado.
Resposta
A função
Tem como gráfico