Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 16
Faça o gráfico da hipérbole por meio dos gráficos das funções que são os ramos superior e inferior da hipérbole.
Passo 1
A questão pede para fazermos o gráfico da hipérbole obtendo duas funções que representam os ramos inferior e superior. Para isso, temos que isolar como função de :
Assim, o ramo superior é dado por
e o ramo inferior por
Passo 2
Em vermelho temos a parte superior (sinal de ) e em verde a parte inferior (sinal de ):
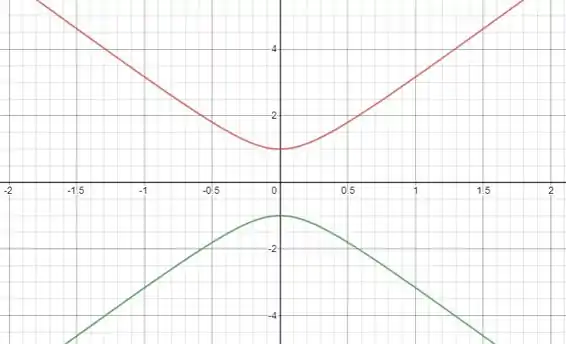
Resposta
Esboço de gráficos.
Exercícios de Livros Relacionados
Identificar as propriedades e características das seguintes funções a partir das suas representações gráficas (domínio, conjunto imagem, raízes, máximos e mínimos, crescimento e decrescimento). f x =
Identificar as propriedades e características das seguintes funções a partir das suas representações gráficas (domínio, conjunto imagem, raízes, máximos e mínimos, crescimento e decrescimento). f x =
Para cada uma das seguintes funções f ( x ) esboce primeiro o gráfico de y = f ( x ) , depois o gráfico de y = f x e finalmente o gráfico de y =f ( x ) 2 + | f x | 2 . f x = x - 2 ( x + 1 )
Para cada uma das seguintes funções f ( x ) esboce primeiro o gráfico de y = f ( x ) , depois o gráfico de y = f x e finalmente o gráfico de y =f ( x ) 2 + | f x | 2 . f x = x 2
Para cada uma das seguintes funções f ( x ) esboce primeiro o gráfico de y = f ( x ) , depois o gráfico de y = f x e finalmente o gráfico de y =f ( x ) 2 + | f x | 2 . f x = - x 2