Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.10 - Ex. 25
25. Determinar algebricamente o domínio das funções , , , e
Faça o gráfico das funções e compare os resultados.
Passo 1
Inicialmente, determinaremos o domínio dessas funções! Para isso, teremos que ver se as funções tem alguma restrição!
Passo 2
Ora, tanto e possuem restrições! NÃO PODEMOS TER VALORES NEGATIVOS DENTRO DE RAIZ DE ÍNDICE PAR.
Para
Para
Já determinamos o Domínio, vamos agora fazer as operações que ele pede!
Para fazermos o domínio dessa função, temos que ver a interseção entre os domínio de e .
O domínio de é de em diante e o domínio de é de em diante, então qual será a interseção?
Ora! Será de 2 em diante, logo o domínio de é:
Faremos , agora:
Faremos o Domínio de
Para , temos:
Para fazermos o domínio da função, primeiro faremos a restrição de ,
Agora faremos a restrição de
Elevando ao quadrado os dois lados, podemos fazer isso, pois dos dois lados temos valores positivos!
O Domínio vai ser dado pela interseção dos dois conjuntos que é:
Passo 3
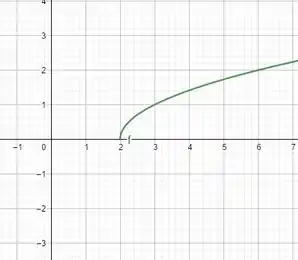
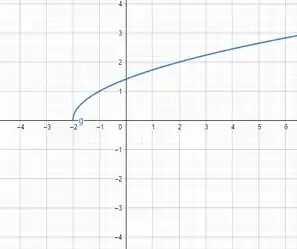
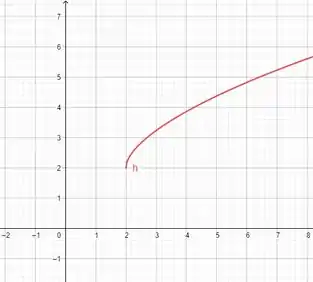
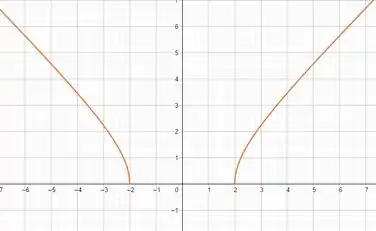
Agora os gráficos! Todos feitos no Geogebra!
