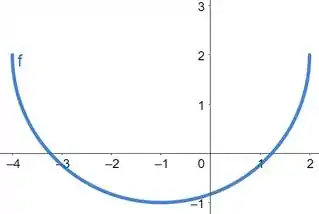
Faça o gráfico da metade inferior do círculo definido pela equação
Passo 1
Como já nos foi informado, a equação dada consiste na equação expandida de uma circunferência. Para podermos obter o gráfico da metade inferior, precisamos discutir um pouco sobre circunferências, para que assim obtenhamos a função desta parte do gráfico. Sendo assim, vamos começar apresentando a equação reduzida de uma circunferência, a qual é dada por:
Em que o ponto é o centro e o raio é . Resolvendo esta equação, obtemos:
A metade inferior é dado pelo sinal negativo da raiz, isto é:
Sendo assim, para obtermos o gráfico, é necessário escrever a equação dada na forma da equação reduzida de uma circunferência. Após isto, resolveremos a equação obtendo apenas a solução cujo sinal da raiz é negativo, e, a partir deste resultado, obteremos o gráfico da função.
Passo 2
Para escrever a equação na forma reduzida, precisamos completar quadrados. Isto é, fazer a seguinte transformação:
Sendo assim, temos:
Logo, é uma circunferência de raio igual a 3 e centro no ponto
Passo 3
Vamos obter agora a equação da metade inferior. Sendo assim, temos:
Passo 4
Agora, basta obter o gráfico da função
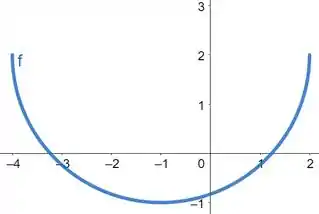
Resposta