Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.1 - Ex. 35
Uma família de curvas que intercepta uma dada família de curvas com um ângulo específico constante é chamada de família isogonal. As duas famílias são chamadas de trajetórias isogonais uma da outra. Se é a equação diferencial da família dada, mostre que a equação diferencial da família isogonal é
Passo 1
E aí? Não se assusta não, vamos matar esse problema rapidinho
Pra começar, vamos imaginar uma curva da família dada, e aí ela vai ter uma reta tangente, ta imaginando?
E aí essa reta tangente forma um ângulo com o eixo .
Agora vamos imaginar a trajetória ortogonal, ela também é uma curva. Ela também vai ter uma reta tangente, mas essa reta forma um ângulo com o eixo .
Ta difícil de imaginar? Cadê as ibagens?
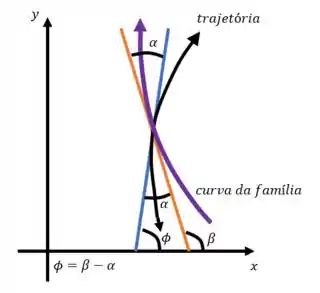
Continuando: no ponto em que a curva roxa e a curva preta se interceptam, as retas tangentes (azul e laranja) vão formar um ângulo entre elas
Existem duas formas de isso acontecer: a primeira é a da imagem que vimos aí em cima, a segunda é assim:
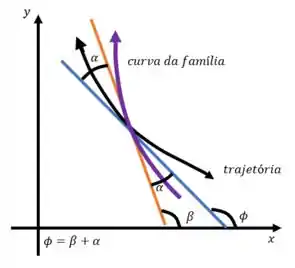
E o que muda de uma pra outra é o
Passo 2
Então, a inclinação da reta tangente à trajetória (reta azul nas duas imagens) é
Lembrando da fórmula de tangente da soma e da diferença: temos , então:
Mas é justamente a derivada da curva roxa, então, , certo? E (dado do enunciado)
E ta provadoooo meu povo!