Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 49
A figura mostra o gráfico de . Identifique cada curva e explique suas escolhas
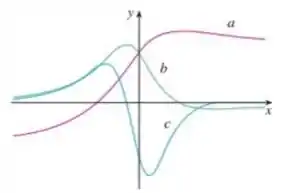
Passo 1
E aí! tudo certinho?
Nesse problema temos três gráficos de funções e nosso objetivo é determinar quem é , e .
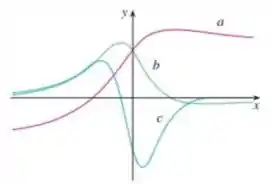
Uma ideia que podemos usar nesse problema é de que a derivada de uma função em um ponto é igual a sua inclinação da reta tangente...
Dessa forma, podemos encontrar os pontos de máximo, ou mínimo, de uma das funções e verificar qual das outras funções corta o eixo nesse mesmo ponto.
OBS: Podemos fazer isso pois em um ponto de máximo ou mínimo, a reta tangente à curva é horizontal e portanto, tem inclinação .
Veja só!
Passo 2
Vamos começar com a curva ...
Perceba que possui apenar um ponto de máximo, isso implica que sua derivada corta o eixo apenas uma vez.
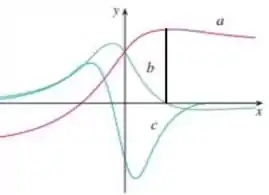
No ponto que é máximo, apenas a curva corta o eixo , por isso, podemos afirmar que é a derivada de
Ainda não sabemos quem é , então vamos analisar a próxima curva!
Passo 3
Analisando a curva , vemos que ela tambem possui um ponto de máximo.
Traçando a reta nesse ponto, chegamos em
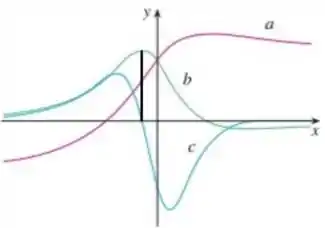
Podemos perceber que quando está no ponto máximo, corta o eixo , logo, pela mesma logica do passo anterior, vemos que é a derivada de .
Aqui já podemos ter uma resposta, mas por via das duvidas, vamos analisar a outra curva.
Passo 4
Por fim, analisando a curva , vemos que aqui temos um ponto de máximo e um de mínimo...
Traçando as retas nesses pontos, temos
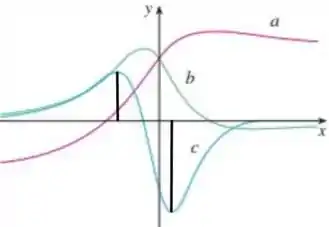
Nos pontos que tem reta tangente horizontal (nos dois pontos de máximo e mínimo) não existe nenhuma outra curva que corta o eixo , logo, não possui nenhuma derivada.
A partir das informações que obtivemos até agora, sabemos que e que , portanto .
Logo, fazendo , vamos obter e .
E então! O que achou? Responde Aí!