Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 61
- Esboce o gráfico de
- Para quais os valores de é diferenciável?
- Encontre uma fórmula para
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu a função e pediu pra gente esboçar o gráfico dela, determinar pra quais valores de essa função é diferenciável e encontrar uma fórmula para sua derivada.
Mas antes de qualquer coisa, vamos analisar a nossa função. Temos um produto de uma função polinominal, , com uma função modular . Como essa função modular é definida por partes, a gente pode escrever a nossa função assim:
Essa função é assim por definição, beleza? A partir disso, vamos conseguir esboçar nosso gráfico, derivar a nossa função e descobrir para quais valores essa derivada é válida.
Vamos lá!
Passo 2
Olhando lá pra definição da nossa função no passo , percebemos que a nossa é igual a , para valores de positivos e iguais a zero (). E que ela é igual a para valores de negativos ().
Então, é como se a gente tivesse metada de duas parábolas, uma com concavidade para baixo e outra com concavidade para cima, cruzando o eixo na origem. Assim:
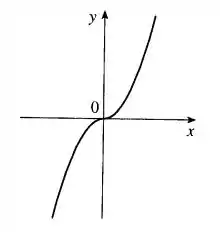
Passo 3
Agora vamos analisar a diferenciabilidade da função. Repare que para , temos , que é uma função polinomial definida para todos os valores de . Isso nos possibilita escrever:
Da mesma forma, para , temos , também definida em todo conjunto dos números reais (por ser uma função polinomial) e que vai nos dar a derivada:
Isso significa que é diferenciável para valores maiores e menores do que zero.
Passo 4
Agora para , precisamos avaliar. E fazemos isso calculando os limites à esquerda e à direita de zero.
Para o limite à esquerda, temos:
Substituindo a função:
Simplificando e aplicando o limite:
Da mesma forma, para o limite à direita, teremos:
Simplificando:
Logo,
Portanto, também é diferenciável em e, consequentemente, é diferenciável para todo .
Passo 5
Juntando esses resultados, vamos ter a fórmula da derivada dessa função:
Isso é a mesma coisa que escrever:
Valeu, galera! Até a próxima! 😉
Resposta
(a) Gráfico no passo
(b) é diferenciável para todo .
(c)