Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 16
Se for a função do Exercício 14, encontre e e use seus gráficos para estimar os intervalos de crescimento e decrescimento e de concavidade de .
Passo 1
Fala aí, pessoal.
Bom, nessa questão teremos que usar a função do exercício 14 para encontra e e usar seus gráficos para estimar os intervalos de crescimento e decrescimento e de concavidade de .
Sendo
Então vamos lembrar o que cada derivada conta pra gente.
A derivada de uma função é entendida como a inclinação da reta tangente a curva do gráfico da função.
Sabendo disso, podemos pensar que quanto mais positiva a derivada estiver, mais rapidamente a função original estará crescendo.
Assim:
Já a derivada de segunda ordem é a inclinação da reta tangente ao gráfico da primeira derivada e ela nos trará informações sobre o sentido da concavidade.
Assim:
O ponto de inflexão acontece onde a derivada de segunda ordem for igual a zero. Assim:
Agora que já sabemos de tudo isso, bora resolver essa questão.
Passo 2
A função que o Exercício 14 nos dá é
Primeiro vamos encontrar as derivadas da nossa função.
Sendo a primeira derivada:
E a segunda:
Maravilha.
Passo 3
Agora vamos usar uma calculadora gráfica para plotar o gráfico de :
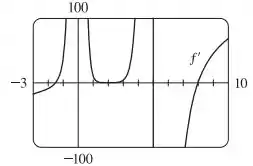
Como já sabemos que o sinal da primeira derivada nos mostrará se a função é crescente ou decrescente, vamos observar seu gráfico e seguir a relação:
Observe que tem seus zeros, ou seja, seus pontos extremos, em
E
Pelo gráfico de , concluímos que está decrescendo em , crescendo em e em , decrescendo novamente em , e finaliza crescendo em .
Passo 4
Estimando um gráfico de
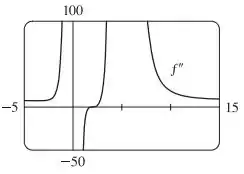
Por esse gráfico, vemos que é o número que zera , e ele mostra que é o único zero de
Assim, é côncava para cima , côncava para baixo em , côncava para baixo em , e côncava para cima, novamente, em .
Vemos que há uma assíntota em e em , e encontramos as concavidades analisando os pontos em que é positiva ou negativa.
Resposta
é:
Decrescente em e em
Crescente em , em e crescendo em
é côncava para cima
côncava para baixo em
côncava para baixo em
e côncava para cima, novamente, em
Há uma assíntota em e em .