Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 74
A função maior inteiro, , é definida como sendo o maior inteiro que é menor do que ou igual a x. Por exemplo: , e . Em cada parte, esboce o gráfico de .
(a)
(b)
(c)
(d)
Passo 1
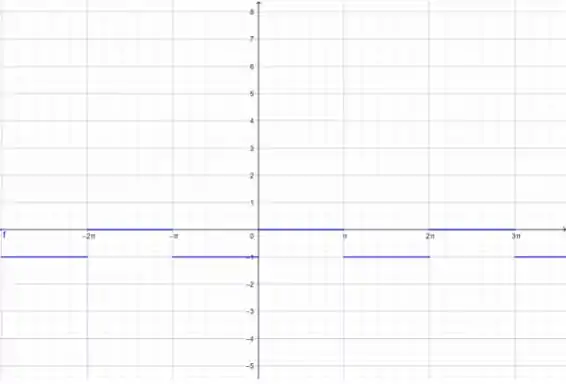
(a) Como vimos no enunciado, vamos sempre pensar no maior inteiro que é menor ou igual a algum número num intervalo. Normalmente, vamos pegar o menor valor do intervalo, ok?
Então, para esboçar , vamos dividir a função em intervalos de para saber qual o menor valor dentro daquele intervalo, ok? Por exemplo, vamos pegar o intervalo . Nesse intervalo, qual o menor valor de ? , certo? Então, a função valerá nesse intervalo!
Vamos fazer isso para todos os intervalos, de 1 em 1 unidade. O gráfico fica assim:
Passo 2
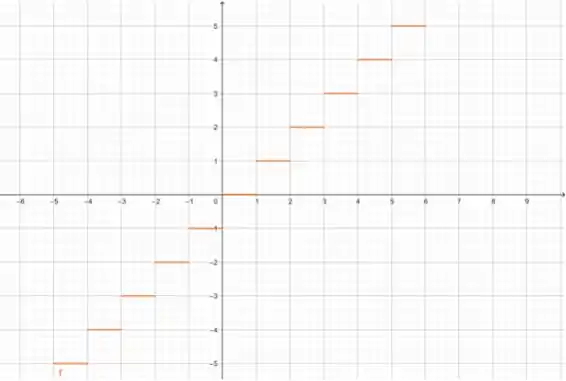
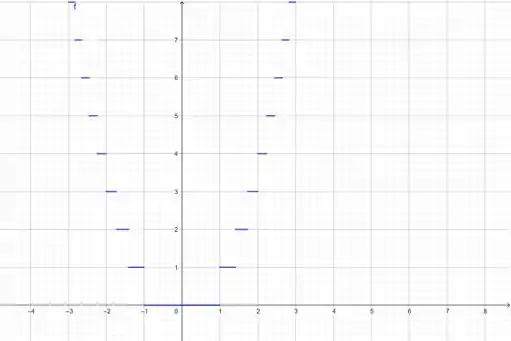
(b) , para esse caso, o raciocínio é o mesmo do passo anterior: vamos dividir em intervalo e olhar para o menor valor que assume no intervalo, porém, agora, vamos ter que a função será o quadrado desse valor. Essa é a única diferença!
Então em , por exemplo, temos que o menor valor é , mas ainda temos que substituir na função:
Então, esse será o valor da função nesse intervalo!! Fazendo isso para todos os outros intervalos:
Passo 3
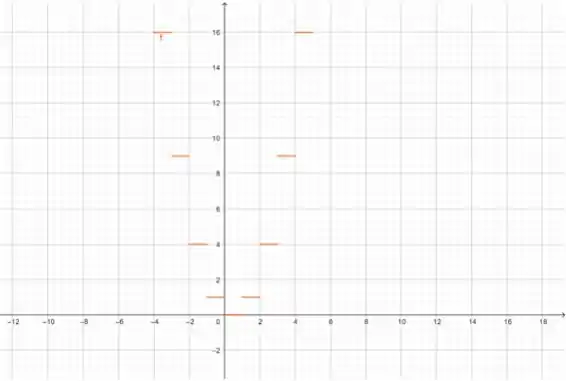
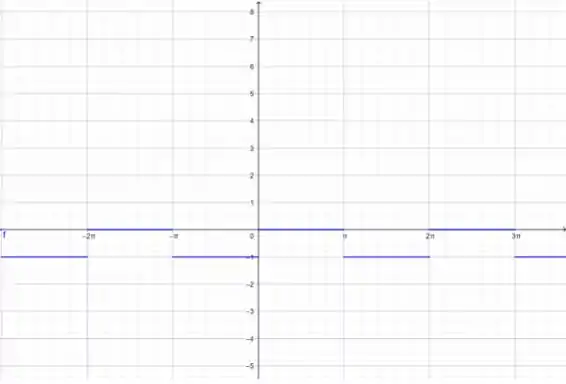
(c) , aqui vamos continuar com a ideia dos intervalos, mas agora, vamos olhar para os intervalos pela função , que tem esse gráfico:
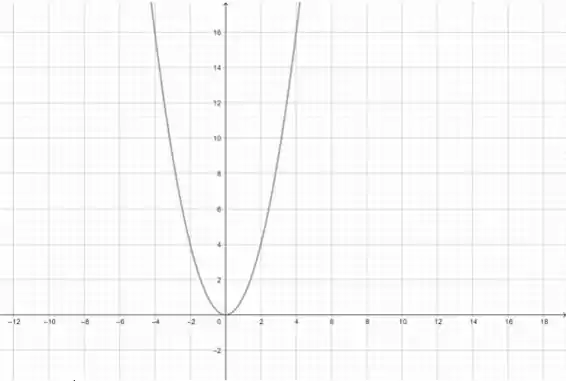
Então, por exemplo, qual o menor valor em que assume? É quando né? Que fica . Vamos usar esse raciocínio para todos os intervalos:
Passo 4
(d) O raciocínio é o mesmo da letra anterior, mas agora para a função .
Então, por exemplo, no intervalo , qual o menor valor que assume? , certo? Que é quando .
Fazendo isso para todos os intervalos:
Prontinho! É só isso!!
Resposta
(a)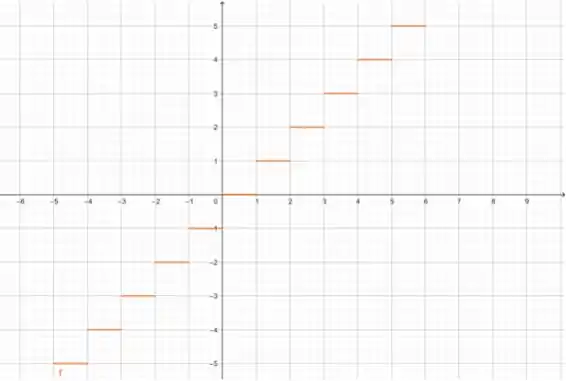 
(b)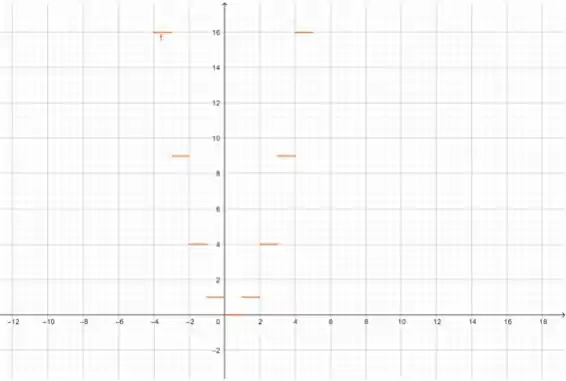 
(c)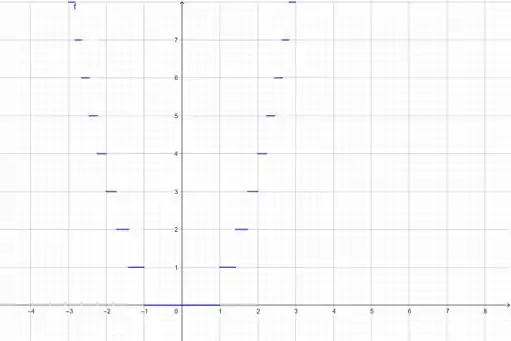 
(d) 