Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 58
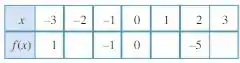
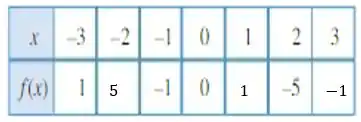
Complete a tabela da figura abaixo de forma que o gráfico de seja simétrico em relação
(a) ao eixo y
(b) à origem
Passo 1
Antes de tudo, precisamos relembrar o que são funções pares e ímpares. E já vamos ver o motivo disso.
Uma função é par quando:
Ou seja, a função possui o mesmo valor à direita e à esquerda do eixo , logo, possui simetria em relação ao !! Olha o motivo de relembrar aí rs.
E uma função é ímpar quando:
Logo, ela possui o oposto do valor à direita e à esquerda de , possuindo simetria em relação à origem.
Então, vamos colocar os valores na tabela de modo à entrar nesses critérios. Ok?
Passo 2
(a) Aqui, deve entrar o critério da função ser par!
Olhando para a tabela:
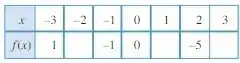
Então, queremos que para qualquer ponto .
Temos 3 pontos a serem preenchidos. Em , e .
Para ser par . Como , .
Para ser par . Como , .
Para ser par . Como , .
A tabela fica:
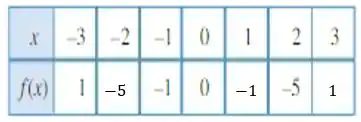
Passo 3
(b) Aqui, deve entrar o critério da função ser ímpar!
Olhando para a tabela:
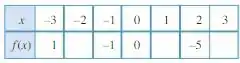
Então, queremos que para qualquer ponto .
Temos 3 pontos a serem preenchidos. Em , e .
Para ser ímpar . Como , .
Para ser ímpar . Como , .
Para ser ímpar . Como , deve ser .
A tabela fica:
Resposta
(a)
(b)