Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 70
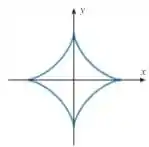
O gráfico da equação , que aparece na figura abaixo, é denominado
hipocicloide quadricúspide.
(a) Use o Teorema 0.2.3 para confirmar que esse gráfico é simétrico em relação ao eixo
x, ao eixo y e à origem.
(b) Encontre uma função f cujo gráfico no primeiro quadrante coincide com a hipocicloide quadricúspide e use um recurso computacional gráfico para confirmar o que foi feito.
(c) Repita (b) para os demais quadrantes.
Passo 1
(a) Vamos ver, primeiro, o que diz o teorema 0.2.3:
- Uma curva plana é simétrica em relação ao eixo y se, e somente se, substituindo-se x por −x em sua equação, obtém-se uma equação equivalente.
- Uma curva plana é simétrica em relação ao eixo x se, e somente se, substituindo-se y por −y em sua equação, obtém-se uma equação equivalente.
- Uma curva plana é simétrica em relação à origem se, e somente se, substituindo-se x por −x e y por −y em sua equação, obtém-se uma equação equivalente.
Então, vamos usar isso para responder ao problema. Só fazer as substituições do teorema e ver em qual dos 3 casos a função se encaixa.
Passo 2
Temos .
Primeiro, vamos substituir por :
Como , o sinal de não fará diferença na equação, pois ele será elevado ao quadrado. Dessa forma, a função não se altera e temos uma simetria em relação ao eixo .
O mesmo vai acontecer para a substituição , pois e o sinal de não fará diferença na equação. Dessa forma, temos simetria em relação ao eixo , também.
Além disso, quando substituímos e também não teremos alteração na equação, pelos mesmos motivos citados acima. Logo, teremos uma simetria em relação à origem, também!
Passo 3
(b) Para acharmos uma função correspondente ao hipocicloide, vamos isolar o e escrevê-lo em função de :
Para tirar o expoente do , vamos elevar a equação toda a :
𝑥233/2
Assim, multiplica e resulta em :
Dessa forma:
Obs.: lembre-se de que, ao tirar uma raiz quadrada, aceitamos valores positivos e negativos como resposta!
Se colocarmos na função, pegaremos os valores positivos de (acima do eixo ). Se colocarmos , pegaremos os valores negativos (abaixo de ).
Como o primeiro quadrante está acima de e acontece para , podemos fazer uma função desse tipo:
O gráfico desse cara é:
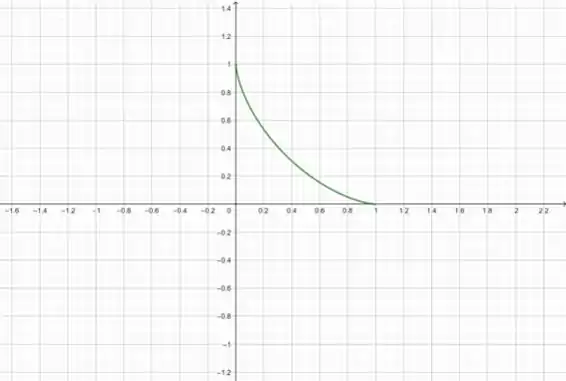
Que é exatamente o primeiro quadrante do hipocicloide!!
Passo 4
(c) Para o segundo quadrante, podemos usar a mesma equação do passo anterior, mas agora temos que . Então:
O gráfico fica:
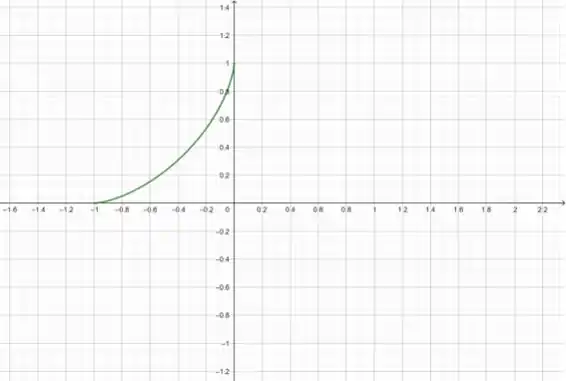
Passo 5
O terceiro quadrante está localizado abaixo do eixo e nos valores para , certo? Então, podemos usar a equação:
O gráfico fica:
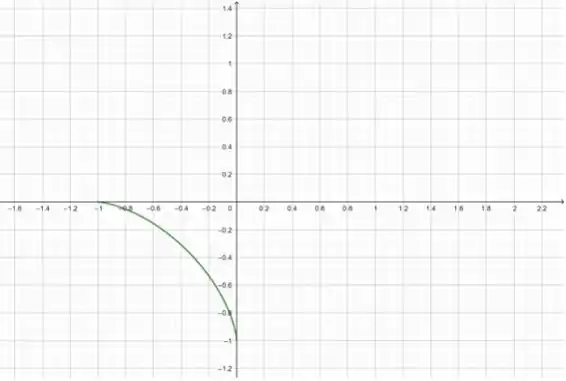
Passo 6
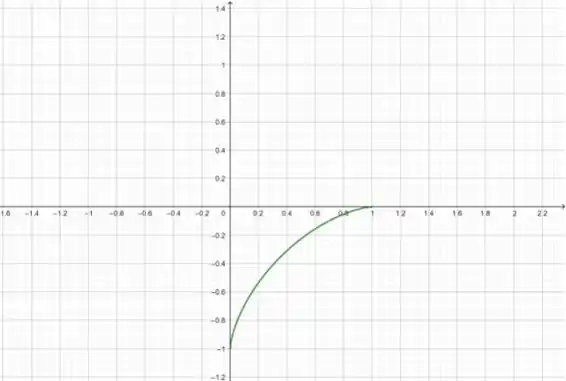
Para o quarto quadrante, podemos usar a mesma equação do passo anterior, mas agora temos que . Então:
O gráfico fica:
Prontinho!
Resposta
(a) Explicação no passo a passo.
(b)
(c)