A função maior inteiro definida para todos os valores de admite um valor máximo local em cada ponto de . Algum desses valores máximos locais poderia ser o mínimo local de ? Justifique sua resposta.

Como o enunciado já diz que todos os pontos dentro do intervalo possuem um valor máximo local, pode-se fazer uma análise geral dessa função nesses valores.

Fazendo o esboço do gráfico de , temos

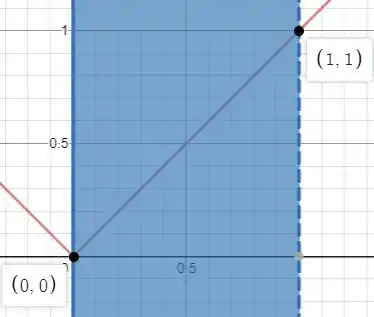
Tal que é possível notar que todos os pontos, além de um valor máximo local, admitem um valor mínimo local pelo fato de que, se atribuirmos um pequeno intervalo aberto em volta de cada valor de , tal valor terá um ponto abaixo à sua esquerda fazendo com que ele seja um máximo local e também terá um ponto acima à sua direita fazendo com que ele seja um mínimo local.

No entanto, em isso não é possível já que um intervalo aberto ao seu redor contém pontos à esquerda de onde a função resulta em .