Exercícios de Máximos e Mínimos - Lista de Exercícios Resolvida
Questão 1
Se:
Identifique os valores extremos locais da função nos domínios dados e informe onde ela os assume.
Alguns desses valores extremos são absolutos? Quais?
Ver solução completaQuestão 3
Considere o polinômio , onde e são constantes reais. É possível determinar valores para e tais que o gráfico de tem um ponto de máximo local quando e um ponto de inflexão quando ?
Ver solução completaQuestão 4
Sendo:
Encontre os intervalos onde a função é crescente e decrescente.
Em seguida, identifique os valores extremos locais da função, se houve, informando onde ela os assume.
Alguns desses valores extremos são absolutos? Quais?
Ver solução completaQuestão 5
Identifique os pontos de máximo e mínimo e de inflexão da função abaixo.
Ver solução completaQuestão 6
- Sejam o valor máximo e o valor mínimo que a função assume em . Então é igual a:
A
B
C
D
E
Ver solução completaQuestão 7
- Sejam o valor máximo e o valor mínimo que a função assume em . Então é igual a:
A
B
C
D
E
Ver solução completaQuestão 8
- Sejam o valor máximo e o valor mínimo que a função assume em . Então é igual a:
A
B
C
D
E
Ver solução completaQuestão 9
- Sejam o valor máximo e o valor mínimo que a função assume em . Então é igual a:
A
B
C
D
E
Ver solução completaQuestão 10
Nos próximos 5 testes assinale “verdadeiro” ou “falso” para cada uma das afirmações.
Para estes testes, seja uma função derivável cuja derivada é dada por
17. A função possui um único ponto crítico.
18. A função possui um único máximo local.
19. A função é descrecente em .
20. A função tem exatamente dois pontos de inflexão.
21. .
Ver solução completaQuestão 12
Questão 5 - Seja . Sabendo que e para todo , determine, caso existam:
(a) assíntotas horizontais e verticais do gráfico de ;
(b) intervalos onde é crescente e intervalos onde é decrescente;
(c) máximos e mínimos locais de ;
(d) intervalos onde o gráfico de é côncavo para cima e intervalos onde o gráfico de é côncavo para baixo;
(e) pontos de inflexão do gráfico de .
Utilizando os resultados dos itens anteriores, esboce o gráfico de .
Ver solução completaQuestão 13
Uma escada de 5 metros de comprimento est ́a apoiada em uma parede vertical. Sabendo-se que o p? é da escada se afasta da parede a uma velocidade de 10 cm/s, qual a velocidade com que cai verticalmente o topo da escada?
Ver solução completaQuestão 14
Seja
- Determine o domínio de
- Explique porque a função é ímpar
- Determine os extremos locais de . (Abscissa e Ordenada) Identificando se eles são máximos ou mínimos. São Globais? Porque?
- Calcule os limites das extremidades de todos os intervalos que compõem o domínio
Questão 16
4. Seja
a) Encontre os intervalos onde é crescente ou decrescente;
b) Determine os pontos de e classifique-os como sendo pontos de máximo, de mínimo ou nem de máximo, nem de mínimo (se existirem);
c) Determine os intervalos onde é côncova para cma e côncava para baixo e os seus pontos de inflexão;
d) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens anteriores.
Ver solução completaQuestão 18
Um homem de 2 m de altura se move em direção a um a poste de luz a uma velocidade de 5 m/s. Do alto deste poste, uma lâmpada ilumina o homem e projeta uma sombra. Quando a distância entre o homem e o poste é de 4 m:
- Com que velocidade a ponta da sobra se move?
- Qual a taxa de variação do comprimento da sombra?
Questão 19
Encontre os pontos críticos da função
Classifique esses pontos críticos localmente, e diga se essa classificação também é global
ou não.
Ver solução completaQuestão 20
Encontre os pontos críticos da função
Classifique esses pontos críticos localmente, e diga se essa classificação também é global
ou não.
Ver solução completaQuestão 21
Prove que para todo vale a seguinte desigualdade:
(Sugestão: estude o crescimento da expressão do lado esquerdo e determine o mínimo absoluto dessa expressão no intervalo dado).
Ver solução completaQuestão 22
Localize os pontos onde ocorrem os extremos absolutos das funções nos intervalos dados:
Ver solução completaQuestão 25
Considere o gráfico da derivada da função representado na figura abaixo:
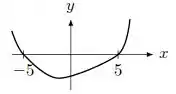
Pode-se afirmar que:
- O ponto é um mínimo local de .
- A função é crescente no intervalo .
- .
- A concavidade do gráfico de é para cima em .
Questão 26
1.
- Existe uma função contínua em e derivável em sem pontos extremos em ?
Questão 28
1.
f. Existe uma função definida em com mínimo global em e máximo global em com para qualquer ?
Ver solução completaQuestão 29
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
b.
Ver solução completaQuestão 31
Seja definida no intervalo fechado . Se é o valor máximo de e se é o valor mínimo de , então o produto é:
Ver solução completaQuestão 32
1.
- Existe uma função contínua em com máximo local no ponto necessariamente satisfaz ?
Questão 34
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
Questão 35
1.
g. Existe uma função contínua em com mínimo global em e máximo global em onde
Ver solução completaQuestão 37
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
f.
Ver solução completaQuestão 38
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
e.
Ver solução completaQuestão 41
1.
k. Uma função composta com e contínuas em necessariamente atinge valores máximos e mínimos globais?
Ver solução completaQuestão 50
Encontre os pontos de máximo e mínimo absolutos (globais) da função no intervalo , bem como seus valores. Explique por que os pontos encontrados são realmente os pontos de máximo e mínimo absolutos da função.
Ver solução completaQuestão 52
Considere a função dada por . A soma dos valores máximo e mínimo de em é igual a:
Ver solução completaQuestão 53
Determine os valores de máximo e mínimo da função na placa triangular fechada e limitada pelas retas ; ; no primeiro quadrante.
Ver solução completaQuestão 55
Em relação à função
É incorreto afirmar que:
- não tem assíntota horizontal.
- tem exatamente um ponto crítico.
- é ponto de máximo local.
- é um ponto de inflexão .
- não tem assíntota oblíquas.
- não tem assíntotas verticais
- o domínio de é .
Não é necessário justificativa.
Ver solução completaQuestão 56
-
Seja a função , determine:
- Os intervalos onde a função é crescente e onde ela é decrescente e os pontos de máximo e mínimo relativos da função:
Ver solução completaQuestão 61
4. Dada a função .
- Os intervalos de crescimento e de decrescimento de .
- Os pontos de máximo e mínimo locais de .
- Os intervalos nos quais é côncova (concavidade voltada para cima) ou com convexa (concavidade voltaa para baixo).
Questão 62
Dada a função
Determine os intervalos de crescimento e de decrescimento, concavidade, os pontos de inexpressão e os pontos de máximo e mínimo.
Ver solução completaQuestão 63
Seja um número real e
Sabe-se que o gráfico da função tem um mínimo local no ponto Op valor de é:
Ver solução completaQuestão 64
Considere a função , definida no intervalo . Determine, se possível, os valores máximo e mínimo locais e absolutos de no intervalo , justificando para isto suas afirmações.
Ver solução completaQuestão 65
Determine, com justificativa, os pontos de máximo e mínimo absolutos da função
no intervalo , e calcule os valores máximo e mínimo respectivos.
Ver solução completaQuestão 66
Seja definida em , cuja derivada tem o seguinte gráfico:
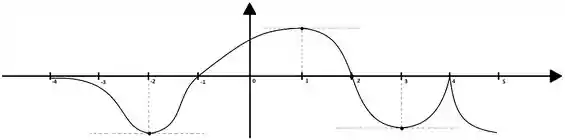
Determine:
(a) Todos os pontos críticos de
(b) Os intervalos onde é crescente e onde é decrescente. Justifique
(c) Todos os pontos de máximo e mínimo local de . Justifique
(d) Todos os pontos de inflexão de . Justifique
Ver solução completaQuestão 67
Seja um número real positivo,
E
Sabe-se que as funções e crescem e decrescem nos mesmos intervalos. O valor mínimo de é:
Escolha uma:
(A) 27
(B) 26
(C) 31
(D) 32
(E) 28
Ver solução completaQuestão 68
Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Questão 69
Seja derivável e suponha que o gráfico da derivada seja dado por:
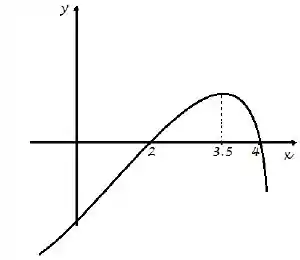
Considere as seguintes afirmações:
- A função tem um mínimo local em e um máximo local em .
- O gráfico de côncavo para baixo em .
- A função tem um ponto de inflexão em .
Então:
- Apenas as afirmações (I) e (III) estão corretas.
- Apenas as afirmações (II) e (III) estão corretas.
- Apenas as afirmações (I) e (II) estão corretas.
- Todas as afirmações estão corretas.
- Apenas a afirmação (I) está correta.
Questão 70
Considere a função definida por
- Determine os intervalos de crescimento e de decrescimento de , caso existam.
- Determine o valor máximo e o valor mínimo da função , caso existam.
- Utilize os itens anteriores para determinar qual dos dois números é maior: ou
Questão 71
Deseja-se construir uma piscina retangular com de área (da superfície) a de distância de um muro. Paralela aos demais lados da piscina será construída uma cerca, deixando um corredor de circulação de de largura.
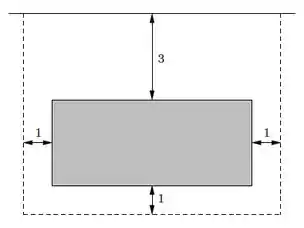
Sabe-se que os lados da piscina paralelos ao muro devem ter no mínimo e no máximo . Sejam e as áreas mínima e máxima que a região cercada pode ter. Então, vale:
Questão 84
Encontre os valores máximos e mínimos globais de f (se existirem) no intervalo dado:
Ver solução completaQuestão 86
O lado de um cubo é medido com um erro máximo possível de 2%. Use diferenciais para estimar o percentagem de erro máximo no volume computado.
Ver solução completaQuestão 88
Seja .Determine, justificando:
(a)As regiões de crescimento e decrescimento de
(b) Os pontos de máximo e mínimo globais, se houver
(c)Os pontos de máximo e mínimo locais, se houver
(d) As regiões de concavidade de
Ver solução completaQuestão 89
3) Encontre os pontos de máximo e de mínimo da função , quando restrita ao intervalo ; ainda, especifique se tais pontos são de máximo/mínimo absoluto ou relativo
Ver solução completaQuestão 91
1.
e. Existe uma função contínua em com máximo global em e mínimo global em ?
Ver solução completaQuestão 96
Considere a função dada por
onde é o domínio
- Encontre e classifique os pontos críticos de no interior do domínio .
- Explique por que os valores extremos absolutos de devem existir em .
- Encontre os valores máximos absolutos e mínimos absolutos de em . Indique os pontos de onde esses valores extremos são atingidos.
Questão 97
2. O custo de produção semanal de celulares, por parte de uma empresa, é dado pela expressão
Sabendo que o preço de venda é por unidade, determine a quantidade de celulares que maximiza o lucro da empresa e o correspondente valor do lucro máximo.
Observação: Lembramos que o lucro total é dado pela expressão , onde é o rendimento das vendas.
Ver solução completaQuestão 98
Considere a função definida para todo real pela expressão
Determine o máximo e mínimo absolutos que atinge no intervalo .
Ver solução completaQuestão 99
O período de um pêndulo simples é dado por:
Sendo L o comprimento do pêndulo, g a aceleração da gravidade e T é medido em segundos. Suponha que o comprimento do pêndulo é medido com um erro máximo de 0,5%. Qual a percentagem de erro máximo no período.
Ver solução completaQuestão 102
Encontre o máximo e o mínimo absoluto da função
na placa retangular (veja figura a seguir).
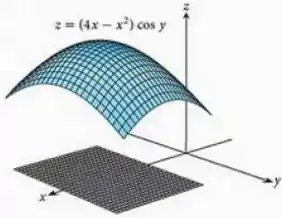
Questão 103
Sejam número real, e .
(a) Classifique os pontos críticos de em função de .
(b) Considere . Encontre os valores máximo e mínimo de no conjunto
Ver solução completaQuestão 104
Seja . Considere as seguintes afirmações:
A função não tem um mínimo nem um máximo local em .
A curva tem um ponto de inflexão em
não existe.
A função é crescente em .
Sobre as afirmações acima, podemos concluir que
e são verdadeiras e e são falsas.
e são verdadeiras e é falsa.
e são verdadeiras e é falsa.
e são verdadeiras e é falsa.
As quatro afirmações são verdadeiras.
Ver solução completaQuestão 105
Considere a função , restrita ao intervalo .
Determine os subintervalos onde é crescente, assim como aqueles onde é decrescente.
Usando as informações do item anterior, determine os pontos de máximo e de mínimo de , indicando se são absolutos(globais) ou relativos(locais).
Ver solução completaQuestão 107
Considere a função , definida a seguir
É correto afirmar que:
Sobre é CORRETO afirmar que:
- O valor mínimo de é e o máximo é
- O valor mínimo de é e o máximo é
- O valor mínimo de é e o máximo é
- O valor mínimo de é e o máximo é
- O valor mínimo de é e o máximo é
Questão 108
Dada a função , considere as afirmações:
não é ponto de mínimo local nem ponto de máximo local de .
é ponto de máximo local de .
é ponto de mínimo local de .
não possui nem mínimo nem máximo locais.
Selecione a opção correta:
A afirmação é verdadeira e as demais são falsas.
A afirmação é verdadeira e as demais são falsas.
A afirmação é verdadeira e as demais são falsas.
As quatro afirmações são falsas.
As afirmações e são verdadeiras e as demais são falsas.
Ver solução completaQuestão 110
Uma determinada máquina deve operar em velocidade constante de rotação. Sua jornada de trabalho é limitada entre rotações por minuto. O custo energético da máquina, medido por , é de por minuto e é consumido em uma razão de por minuto. O operador da máquina é pago a um custo de reais por minuto. Considere que a velocidade de rotação constante é obtida logo que a máquina entre em funcionamento. Determine para cada valor de , a velocidade de rotação que se obtém o custo mínimo consumido pela máquina em uma jornada de trabalho, sabendo que
Ver solução completaQuestão 111
Seja derivável até segunda ordem em tal que Seja também
Dê o que se pede:
- Determine , se possível, de modo que seja contínua no ponto .
- Determine se o ponto é o ponto mínimo, máximo, de inflexão ou nenhum dos casos.
Questão 112
5) Considere a função , onde . Encontre os valores de máximos e mínimos locais (se houver). A função tem um valor de mínimo global? Encontre uma equação para a assíntota oblíqua de .
Ver solução completaQuestão 113
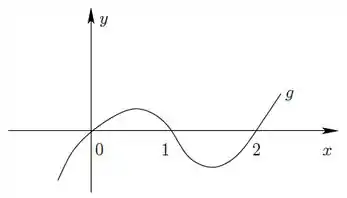
Se é a derivada de uma função , conclui-se que, necessariamente,
- é um número positivo
- possui três pontos de inflexão
- possui um único ponto de máximo local
- possui pelo menos duas raízes reais distintas
Questão 114
4) Se um resistor de estiver ligado a uma pilha de volts com resistência interna ohms, então a potência (em watts) no resistor externo é
Se e forem fixados, mas variar, qual é o valor máximo da potência.
Ver solução completaQuestão 115
Dada a função , considere as afirmações abaixo:
é decrescente no intervalo ;
é côncava para baixo em
possui um máximo local em .
Podemos concluir que
As três afirmações são verdadeiras
As afirmações e são verdadeiras e a afirmação falsa.
As afirmações e são verdadeiras e a afirmação falsa.
A afirmação é verdadeira e as afirmações e falsa.
As três afirmações são falsas.
Ver solução completaQuestão 116
Seja . Considere as seguintes afirmações:
A curva não tem assíntotas verticais.
A função tem um máximo local, mas não tem um mínimo local.
A função tem um mínimo local, mas não tem um máximo local.
O gráfico é côncavo para baixo.
O gráfico de tem um único ponto de inflexão.
A respeito das afirmações acima, podemos concluir que
e são verdadeiras, e são falsas.
e são verdadeiras e e são falsas.
e são verdadeiras e e são falsas.
e são verdadeiras e e são falsas.
e são verdadeiras e e são falsas.
Ver solução completaQuestão 117
Dada a função , considere as afirmações:
não é ponto de mínimo local nem ponto de máximo local de .
é ponto de máximo local de .
é ponto de mínimo local de .
não possui nem mínimo nem máximo locais.
Selecione a opção correta:
As quatro afirmações são falsas.
A afirmação é verdadeira e as demais são falsas.
As afirmações e são verdadeiras e as demais são falsas.
A afirmação é verdadeira e as demais são falsas.
A afirmação é verdadeira e as demais são falsas.
Ver solução completaQuestão 118
Seja uma função sobre a qual sabe-se apenas que é duas vezes diferenciável e
Considere as seguintes afirmações:
necessariamente é um valor de mínimo local.
necessariamente é um valor de mínimo global.
necessariamente é um ponto de inflexão.
necessariamente é um valor de mínimo local.
As afirmações e são verdadeiras
As afirmações e são verdadeiras
As afirmações e são verdadeiras
A afirmação é verdadeira
A afirmação é verdadeira
Ver solução completaQuestão 119
Assinale somente as alternativas com afirmações corretas.
(Haverá desconto na nota desta questão caso alternativas incorretas sejam assinaladas.)
Escolha uma ou mais:
a) Se é uma função qualquer tal que , então existe tal que
b) Se e são função deriváveis definidas em e se em , então em
c) Se é uma função que admite derivada até segunda ordem em toda a reta, tal que e , então
d) Se e são polinômios, tais que grau(), então possui assíntotas vertical, ou seja, existe tal que ou
e) Se é uma função derivável até segunda ordem tal que tem duas soluções reais distintas, então tem algum ponto de extremo (máxima ou mínimo) local.
f) Se é uma função tal que para todo então .
Ver solução completaQuestão 120
Estude a função dada por
1) Estude o crescimento de , determinando os pontos de máximo e de mínimo locais e globais de , se existirem.
2) Estude a concavidade de
3) Determine as assíntotas do gráfico de , se existirem.
4) Faça um esboço do gráfico de
Ver solução completaQuestão 121
Seja ABCD um retângulo com diagonal medindo cm. Colamos os lados e para obter um cilindro circular, conforme figura abaixo.
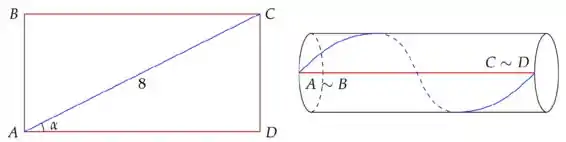
Sendo o ângulo , determine:
1. o volume do cilindro como função exclusivamente de
2. todos os pontos críticos de .
Ver solução completaQuestão 122
O gráfico da função derivada de uma função contínua é dado abaixo
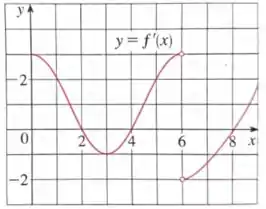
- Em quais pontos a função tem um máximo local? E em quais um mínimo local?
Questão 123
5. Determina valores de , , , para os quais a função definida por
Para um ponto de máximo local em , um ponto de mínimo local em , e
Ver solução completaQuestão 124
5. Considere a função .
- Determine os intervalos nos quais é crescente e decrescente.
- Determine os intervalos nos quais é côncova (concavidade voltada para cima) ou com convexa (concavidade voltaa para baixo).
- Determine os pontos de máximo e mínimo locais de .
Questão 125
Encontre todos os pontos de máximos, mínimos ou pontos de sela da função:
Ver solução completa
Questão 126
ME05) Seja , definida em toda reta real. O número de soluções da equação no intervalo é:
Questão 127
Localize os pontos onde ocorrem os extremos absolutos das funções nos intervalos dados:
Ver solução completaQuestão 128
Determine os pontos de máximo e mínimos locais, e pontos de sela da função
Ver solução completaQuestão 130
Uma indústria farmacêutica está testando o uso combinado de dois princípios ativos para o tratamento de uma doença. Suponha que seja o tempo
necessário para que a medicação faça efeito, onde
e são as massas em mg de cada princípio ativo. Determine para que a
medicação tenha o menor tempo de resposta.
Ver solução completaQuestão 131
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
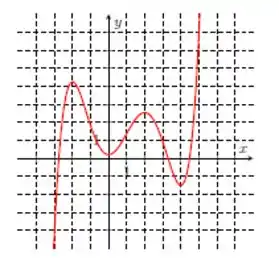
Questão 132
Defina ponto crítico. Conforme videoaula, dê uma definição diferente que é usada por outros professores e livros.
Ver solução completaQuestão 133
A demanda de um certo produto é unidades por mês quando o preço é p reais a unidade.
(d) Discuta o significado econômico do fato de que a função de gasto intercepta 2 vezes o eixo x.
Ver solução completaQuestão 134
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
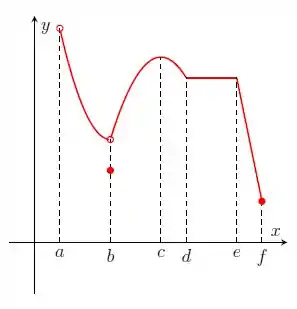
Questão 141
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(b)
Ver solução completaQuestão 142
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(c)
Ver solução completaQuestão 144
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(d)
Ver solução completaQuestão 145
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(e)
Ver solução completaQuestão 146
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(f)
Ver solução completaQuestão 147
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(b)
Ver solução completaQuestão 148
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(a)
Ver solução completaQuestão 149
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(e)
Ver solução completaQuestão 150
Considere a função , definida em seu maior domínio possível.
c) Determine em quais intervalos a função é crescente e em quais ela é decrescente, apresentando os pontos de máximo ou mínimo locais, se existirem.
Ver solução completaQuestão 151
Um retângulo deve ser inscrito na elipse . Quais devem ser as dimensões do retângulo, para que sua área seja máxima?
Ver solução completaQuestão 152
Se é uma função diferenciável tal que e em .
a) Qual o ponto de máximo global de Justifique.
Ver solução completaQuestão 153
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(f)
Ver solução completaQuestão 154
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(h)
Ver solução completaQuestão 155
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(a)
Ver solução completaQuestão 156
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(b)
Ver solução completaQuestão 157
Determine as dimensões do cone circular reto de volume mínimo que pode ser circunscrito a uma esfera de de raio.
Ver solução completaQuestão 159
Determine as dimensões do cilindro circular reto de maior volume possível que esteja inscrito em um cone circular reto de volume fixo.
Ver solução completaQuestão 160
Determine as dimensões do retângulo de área máxima que pode ser inscrito em um triângulo de de base e de altura, estando um dos lados do retângulo sobre a base do triângulo.
Ver solução completaQuestão 162
Considere a função cuja derivada é
(d) os pontos de máximo local de f
Ver solução completaQuestão 163
3(b) Encontre os pontos no interior de , caso existam, onde a função alcança valores extremos locais
Ver solução completaQuestão 164
3(c) Use multiplicadores de Lagrange para achar possíveis pontos na fronteira de onde alcança valores extremos.
Ver solução completaQuestão 165
Determine os máximos e mínimos absolutos da função na
região limitada pela curva
Ver solução completaQuestão 166
Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Questão 168
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
b.
Ver solução completaQuestão 169
7.26. (P2, 2016) Seja definida no intervalo fechado . Se é o valor máximo de e se é o valor mínimo de , então o produto é
a. ;
b. ;
c. ;
d. ;
e. .
Ver solução completaQuestão 171
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
g.
Ver solução completaQuestão 173
1.
- Existe uma função contínua em que não atinge nem máximo nem mínimo?
Questão 176
Considere a função .
Determine os máximos e mínimos de no compacto .
Ver solução completaQuestão 177
Seja o valor mínimo de e o máximo valor de . Encontre
a)
b)
c)
d)N.A
Ver solução completaQuestão 181
15. Mostre que é um ponto crítico da função , mas não tem um valor extremo local neste ponto.
Ver solução completaQuestão 183
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
Questão 185
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
b)
Ver solução completaQuestão 186
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
c)
Ver solução completaQuestão 187
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
d)
Ver solução completaQuestão 188
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
e)
Ver solução completaQuestão 189
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
f)
Ver solução completaQuestão 190
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
g)
Ver solução completaQuestão 191
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
i)
- A função assume máximo ou mínimo absoluto? Em caso afirmativo, quais são estes valores?
Questão 192
6. Determine os pontos críticos da função dada e classifique-os em máximo e mínimo locais:
Ver solução completaQuestão 193
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
A função assume máximo ou mínimo absoluto? Em caso afirmativo, quais são estes
valores?
Ver solução completaQuestão 194
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
A função assume máximo ou mínimo absoluto? Em caso afirmativo, quais são estes
valores?
Ver solução completaQuestão 195
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
e) A função assume máximo ou mínimo absoluto? Em caso afirmativo, obtenha as equações das assíntotas horizontais ao gráfico de .
Ver solução completaQuestão 196
Esboce o gráfico de , com . Quais são os valores máximos e mínimos globais desta função?
Ver solução completaQuestão 197
Mostre que é um ponto crítico da função , com . É verdade que esta função tem um ponto máximo ou mínimo em ? Explique!
Ver solução completaQuestão 199
Encontre todos os números que satisfaçam à conclusão do Teorema do Valor Médio nos seguintes casos:
Questão 200
Dividir o número em duas partes tais que o produto de uma pelo quadrado da outra seja o
maior possível.
Ver solução completaQuestão 201
Deseja-se fazer um cartaz usando uma folha de papel retangular de de área. As margens no topo e na base devem medir e nos lados, . Determine as dimensões dessa folha, sabendo que a área impressa é máxima.
Ver solução completaQuestão 203
Determinar os pontos dos extremos relativos e os pontos de curvatura máxima da curva
De qual lado dos extremos relativos encontram-se os pontos de curvatura máxima? Qual é o valor da curvatura máxima? Compare-o com o valor da curvatura nos extremos relativos.
(Sugestão: Esboçar a curva aproximadamente!)
Ver solução completaQuestão 204
Considere a função
Determine suas assíntotas (caso existam), intervalos de crescimento e decrescimento, pontos críticos, máximos e mínimos locais (caso existam), analise a concavidade e encontre pontos de inflexão (caso existam) e, por fim, esboce o gráfico da função, destacando os elementos anteriores.
Ver solução completaQuestão 205
Um ponto é chamado máximo local de se existe tal que
Naturalmente, todo ponto de máximo de é um ponto de máximo local de . Supondo que é um ponto de máximo local de onde a derivada existe, resolva os itens abaixo.
a)Usando a desigualdade acima, verifique que a derivada lateral à direita satisfaz
b) Repetindo o argumento, verifique que a derivada lateral à esquerda satisfaz
c)Lembrando que as derivadas laterais coincidem, conclua que
Ver solução completaQuestão 206
Para cada uma das funções abaixo, determine os pontos críticos, classifique-os como
máximos ou mínimos locais, quando for o caso, e determine os intervalos onde f é crescente e decrescente
Ver solução completaQuestão 207
Toda função contínua definida em tem ponto máximo e de mínimo. Use os 3 exercícios anteriores para descrever a estratégia para encontrar os pontos de máximo e de mínimo desta função.
Ver solução completaQuestão 208
- Considere a dada por e suas derivadas e
- Determine, se houver, os pontos de máximo e de mínimo locais de . É possível garantir que eles são máximo ou de mínimos globais? Justifique.
Ver solução completaQuestão 209
Um retângulo deve ser inscrito em uma semicircunferência de raio . Qual é a maior área que o retângulo pode ter e quais são as suas dimensões?
Ver solução completaQuestão 210
Explique porque o ponto é um ponto de mínimo da função . O que acontece com a derivada neste ponto?
Ver solução completaQuestão 211
Seja , com , a equação de uma reta que passa pelo ponto (2,3).
d) explique porque somente a teoria desenvolvida até agora não nos permite concluir que A tem um ponto de mínimo
e) verifique que a função tende para infinito quando ou
Ver solução completaQuestão 212
Para cada uma das funções abaixo, determine os pontos críticos, classifique-os como
máximos ou mínimos locais, quando for o caso, e determine os intervalos onde f é crescente e decrescente
Ver solução completaQuestão 213
Para cada uma das funções abaixo, determine os pontos críticos, classifique-os como
máximos ou mínimos locais, quando for o caso, e determine os intervalos onde f é crescente e decrescente
Ver solução completaQuestão 214
Mostre que a função tem um máximo absoluto em . Usando agora o fato de que e que a função é crescente, conclua que
Ver solução completaQuestão 215
Sejam uma constante positiva e satisfazendo:
a) Determine os pontos críticos, intervalos em que é crescente e intervalos em que é decrescente.
b) Determine e use o teste da derivada segunda para classificar os pontos críticos de .
c) Determine os intervalos em que a concavidade do gráfico de é para cima, os intervalos em que ela é para baixo e os pontos de inflexão do gráfico de .
d) Usando os itens anteriores, faça um esboço do gráfico de supondo que ; ; .
Ver solução completaQuestão 216
Analise os interalos de crescimento e decrescimento de , definida em , para concluir que:
Ver solução completaQuestão 217
Determine os pontos críticos, intervalos de crescimento e decrescimento, bem como os pontos de máximo de mínimo locais das funções abaixo:
h)
Ver solução completaQuestão 218
Seja .
b) Existem e que tornam um ponto de inflexão horizontal? Em caso afirmativo, determine-os.
Ver solução completaQuestão 219
Mostre que a curva tem três pontos de inflexão e que todos ficam sobre uma mesma reta.
Ver solução completaQuestão 220
Para quais valores de o polinômio tem dois pontos de inflexão? E um ponto de inflexão? E nenhum?
Ver solução completaQuestão 221
Seja .
- Que condições e devem satisfazer para que seja um ponto de inflexão de ? Justifique.
Questão 222
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
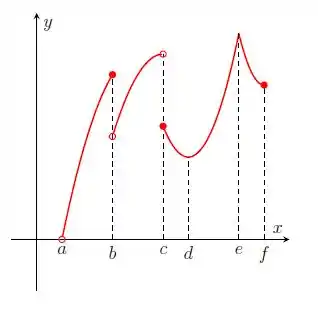
Questão 223
Seja . O ponto 2 é ponto de
a. máximo local mas não global.
b. mínimo local mas não global.
c. máximo global.
d. mínimo global.
e. inflexão.
Ver solução completaQuestão 224
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
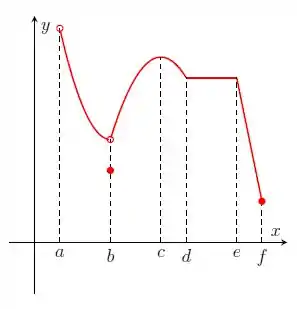
Questão 225
Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo máximo local é máximo absoluto
- Todo ponto de máximo absoluto é um ponto de máximo local
- Todo ponto de máximo locla é ponto de máximo absoluto
- Se possui máximo local, então possui máximo absoluto
- É possível que tenha infinitos pontos de máximo locais e não ter ponto de máximo absoluto
- Toda função possui máximo absoluto em um intervalo fechado
- Toda função que possui máximo absoluto em um intervalo fechado é contínua
- Se possui máximo absoluto, então possui mínimo absoluto
- Se é contínua, então possui mínimo absoluto
Questão 226
Localize os pontos onde ocorrem os extremos absolutos das funções nos intervalos dados:
Ver solução completaQuestão 227
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
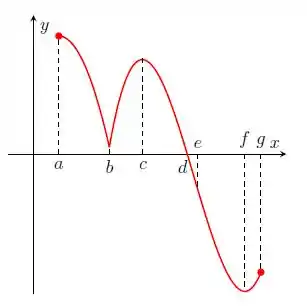
Questão 228
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
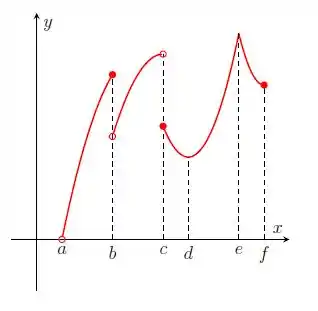
Questão 229
Admitindo as propriedades das funções potências, é possível resolver esse exercício sem o auxílio computacional?
Ver solução completaQuestão 230
A soma de dois números positivos reais é . Encontre o maior valor que pode atingir seu produto.
a)
b)
c)
d)N.A
Ver solução completaQuestão 231
Determine os pontos de máximo e mínimo da função restrita à elipse . Determine os valores máximos e mínimos.
Ver solução completaQuestão 235
Considere a função . Sabe-se que -3 é ponto crítico e que -16 é valor crítico de . Determine b e c.
Ver solução completaQuestão 239
Seja .
(a) Podemos garantir que a função possui máximo absoluto e mínimo absoluto em ? Justifique.
(b) Determine o valor máximo absoluto e o valor mínimo absoluto de em , se possível. Justifique.
Ver solução completaQuestão 241
Questão: (8 pontos) Considere a função definida no intervalo . Determine, caso exista, os seus valores máximo e mínimo globais.
Ver solução completaQuestão 242
5) A função possui:
- máximos locais e mínimo local.
- máximo local e mínimo local.
- mínimos locais e máximos locais.
- máximos locais e mínimo local.
Questão 243
Para cada uma das funções abaixo, determine os pontos críticos, classifique-os como
máximos ou mínimos locais, quando for o caso, e determine os intervalos onde f é crescente e decrescente
Ver solução completaQuestão 244
3) Uma janela tem a forma de um semicírculo encimado por um retângulo. Se o perímetro da janela deve ser de , determine os lados do retângulo que proporcionam área máxima para a janela.
Ver solução completaQuestão 245
2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(b)
Ver solução completaQuestão 246
2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(c)
Ver solução completaQuestão 247
2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(e)
Ver solução completaQuestão 248
2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(d)
Ver solução completaQuestão 251
Prove o Teorema de Ana Lin: seja uma função contínua em e diferenciável em . Seja o único ponto crítico de nesse intervalo e suponha que a função tenha um mínimo local em . Então a função tem um mínimo global em .
Ver solução completaQuestão 253
3. Para cada função abaixo determine: pontos críticos, extremos relativos (isto é, máximos e mínimos locais), intervalos de crescimento e de decrescimento.
b)
Ver solução completaQuestão 255
Para cada função abaixo determine: pontos críticos, extremos relativos (isto é, máximos e mínimos locais), intervalos de crescimento e de decrescimento.
Ver solução completaQuestão 256
Seja
(a) Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo e mínimo.
Ver solução completaQuestão 257
Seja uma função qualquer derivável em todos os pontos de . Considere as afirmativas abaixo:
- Se , então com certeza não é um máximo local de .
- Se , então com certeza é um mínimo ou máximo local de .
É verdadeira ou são verdadeiras:
- Somente a afirmativa (I).
- Somente a afirmativa (II).
- Nenhuma das afirmativas.
- As afirmativas (I) e (II).
Questão 259
Um fazendeiro deve cercar dois pastos retangulares, de dimensões e , com um lado comum . Se cada pasto medir de área, determine as dimensões e , de forma que o comprimento da cerca seja mínimo.
Ver solução completaQuestão 260
Seja , em que é a função cujo gráfico é ilustrado ao lado
- Em que valor atinge seu valor máximo?
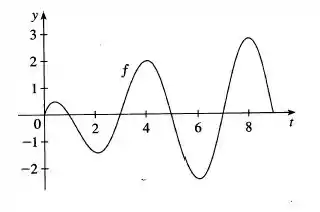
Questão 261
Seja , em que é a função cujo gráfico é ilustrado ao lado
- Em que valores de ocorrem os valores máximos e mínimos locais de ?
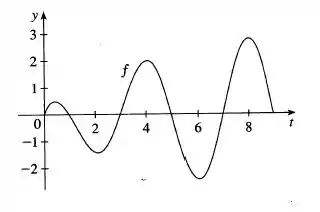
Questão 262
Para a função contínua abaixo dada no respectivo intervalo fechado, determine os máximos e mínimos globais.
em
Ver solução completaQuestão 263
Sejam e dadas por
Onde e são constantes reais positivas.
Prove que é o valor máximo de .
Ver solução completaQuestão 264
Proceda de maneira análoga ao exercício acima para definir o conceito de mínimo local de . O que se pode dizer sobre a derivada de em um ponto de mínimo local?
Ver solução completaQuestão 265
Dê um exemplo de uma função com domínio , que não possua nem máximo e nem mínimo absolutos.
Ver solução completaQuestão 266
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
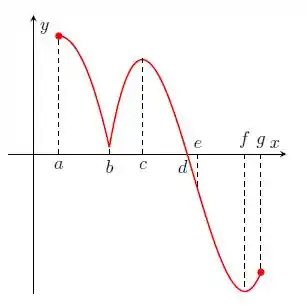
Questão 267
Encontre todos os pontos de máximos, mínimos ou pontos de sela da função:
Ver solução completaQuestão 268
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
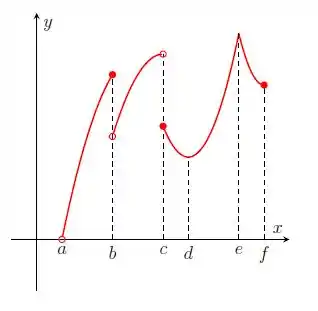
Questão 269
4 – Considere uma reta vertical que intercepta os gráficos e nos pontos e , respectivamente. Sabendo que o comprimento do segmento é o menor possível, determine o valor de .
Ver solução completaQuestão 270
43. Prove que cada um dos conjuntos abaixo admite máximo e mínimo.
a)
Ver solução completaQuestão 271
43. Prove que cada um dos conjuntos abaixo admite máximo e mínimo.
b)
Ver solução completaQuestão 272
Encontre todos os pontos de máximos, mínimos ou pontos de sela da função:
Ver solução completaQuestão 273
Considere a função . Assinale a única alternativa verdadeira.
A função tem valor máximo local e também tem valor mínimo local.
A função tem valor mínimo local, mas não tem valor máximo local.
A função não tem nem valor máximo local nem valor mínimo local.
A função tem valor máximo local, mas não tem valor mínimo local.
A função tem infinitos valores máximos locais e também infinitos valores mínimos locais.
Ver solução completaQuestão 274
Seja , onde , , são constantes reais. Considere as seguintes afirmações:
- Existe tal que .
- possui ao menos um ponto crítico.
- possui exatamente um ponto de inflexão.
- Se então é injetora.
É sempre correto somente o que se afirma em:
- , e
- e
- e
- , e
- e
Questão 275
Dada a função , obtenha seus pontos de máximo e mínimo relativos e absolutos, sabendo-se que o domínio é D = [0; 6].
Ver solução completaQuestão 276
A altura de um objeto que se desloca verticalmente é dada por
,
com h em m e t em segundos. Determine: (b) sua altura máxima e quando esta ocorre;
Ver solução completaQuestão 277
A altura de um objeto que se desloca verticalmente é dada por
,
com h em m e t em segundos. Determine: (c) sua velocidade quando .
Ver solução completaQuestão 278
Um objeto de massa m é arrastado ao longo de um plano horizontal sobre a ação de uma força
F agindo ao longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano,
então a intensidade da força é
onde µ, é uma constante chamada coeficiente de atrito. Para qual valor de a F é a menor
possível?
Ver solução completaQuestão 279
1.
c. Um função contínua em com mínimo local no ponto necessariamente tem pontos críticos em ?
Ver solução completaQuestão 280
2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
d.
Ver solução completaQuestão 284
Determine:
O número real positivo cuja soma com o inverso do seu quadrado seja mínima.
Ver solução completaQuestão 285
Seja com e possui mínimo local no ponto e máximo local em O valor de
Ver solução completaQuestão 286
Ache o ponto de mínimo de
no intervalo . Use isso para provar que
, para todos
Ver solução completaQuestão 287
Considere a função e determine
- O domínio de
- Os intervalos onde é estritamente crescente e decrescente
- Os intervalos de convexidade (concavidade pra cima) e concavidade (concavidade pra baixo)
- Os pontos de máximo e mínimo (se houver)
- As assíntotas verticais e horizontais (se houver)
Questão 288
Seja uma função derivável definida no intervalo . O gráfico abaixo é o gráfico da derivada de , ou seja, o gráfico de :
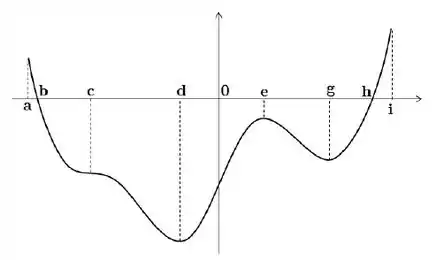
Decida se cada uma das afirmações abaixo é verdadeira ou falsa, justificando sua resposta
c) A função tem um mínimo local em
Ver solução completaQuestão 289
Considere a função . Sabe-se que é o único ponto crítico de . Determine e .
Ver solução completaQuestão 292
Um barco deixa as docas às 14h e viaja para o sul com velocidade de 20km/h. Outro barco
estava rumando para o leste a 15km/h e alcança a mesma doca às 15h. Em que momento os
dois botes estavam mais próximos um do outro?
Ver solução completaQuestão 293
Jane está em um barco a 2 km da costa e deseja chegar a uma cidade litorânea localizada 6 km
ao longo de uma linha costeira retilínea desde o ponto (na costa) mais próximo do barco. Ela
rema a 2 km/h e caminha a 5 km/h. Onde ela deve aportar para chegar à cidade no menor
tempo possível?
Ver solução completaQuestão 294
Certo lago pode suportar uma população máxima de peixes. Considerando que há poucos peixes no lago, sabe-se que a taxa de crescimento populacional será proporcional ao produto da população existente pela diferença da população existente a partir de , ou seja, , onde é a taxa de crescimento para uma população de dimensão .
Pergunta-se: Para que população a taxa de crescimento será máxima?
Ver solução completaQuestão 295
A concentração de certa substância química no fluxo sanguíneo em horas após ter sido injetado no músculo é dada por
Em que instante a concentração é máxima? Qual é a concentração máxima?
Ver solução completaQuestão 296
Suponha que e são funções diferenciáveis no ponto e que e . Se e atingem um valor máximo local em , então mostre que também atingem um valor máximo local em .
Ver solução completaQuestão 297
Determine qual(is) são os pontos críticos da função .
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 298
Dada a função , determine:
Ponto(s) de máximo relativo (local), caso existam;
Ver solução completaQuestão 299
Dada a função , determine:
Ponto(s) de mínimo relativo (local), caso existam;
Ver solução completaQuestão 304
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
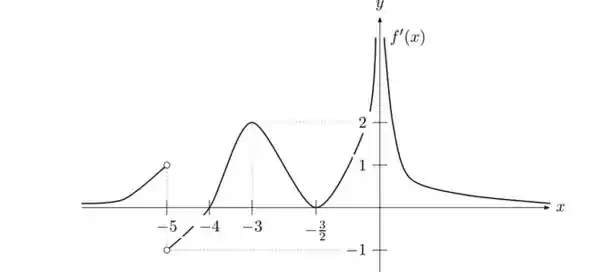
Responda, justificando, o que se pede:
c) Os pontos de máximos e mínimos relativos (locais) caso existam;
Ver solução completaQuestão 305
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
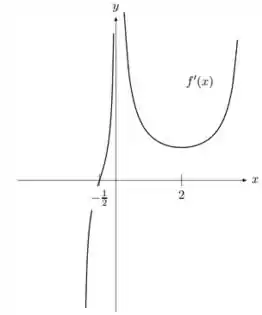
Responde o que se pede:
c) Os pontos de máximos e mínimos relativos (locais) caso existam;
Ver solução completaQuestão 306
Que valor de faz ter:
- Um mínimo local em ?
- Um ponto de inflexão quando
Questão 308
Em cada um dos itens abaixo, encontre os pontos críticos da função (se existirem)
Ver solução completaQuestão 309
Em cada um dos itens abaixo, encontre os pontos críticos da função (se existirem)
Ver solução completaQuestão 310
Em cada um dos itens abaixo, encontre os pontos críticos da função (se existirem)
Ver solução completaQuestão 311
Em cada um dos itens abaixo, encontre os pontos críticos da função (se existirem)
Ver solução completaQuestão 312
Em cada um dos itens abaixo, encontre os pontos críticos da função (se existirem)
Ver solução completaQuestão 313
Em cada um dos itens abaixo, encontre os pontos críticos da função (se existirem)
Ver solução completaQuestão 322
Determine o maior produto de 3 números reais positivos cuja soma é 100. Exiba tais números.
Ver solução completaQuestão 323
Sendo α, β e γ os ângulos de um triângulo, calcule o valor máximo de .
Ver solução completaQuestão 326
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Questão 327
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Questão 328
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Use as informações obtidas nos itens 1)-3) para esboçar o gráfico de
Ver solução completaQuestão 329
Determine as dimensões do paralelepípedo de volume máximo, com faces paralelas aos planos coordenados, inscrito no elipsóide .
Ver solução completaQuestão 330
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Questão 331
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Use as informações obtidas nos itens 1)-3) para esboçar o gráfico de
Ver solução completaQuestão 332
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Use as informações obtidas nos itens 1)-3) para esboçar o gráfico de
Ver solução completaQuestão 333
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Use as informações obtidas nos itens 1)-3) para esboçar o gráfico de
Ver solução completaQuestão 334
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Use as informações obtidas nos itens 1)-3) para esboçar o gráfico de
Ver solução completaQuestão 336
Analise
- Os intervalos nos quais é crescente ou decrescente;
- Os valores máximo e mínimo locais de ;
- Os intervalos de concavidade e os pontos de inflexão;
Use as informações obtidas nos itens 1)-3) para esboçar o gráfico de
Ver solução completaQuestão 339
Obtenha os intervalos onde a função é côncava para cima ou para baixo
Ver solução completaQuestão 342
3) Considere a função .
a) Mostre que o domínio de é precisamente o intervalo fechado
b) Determine os pontos de máximo e mínimo absolutos de . Ainda, calcule os valores de máximo e mínimo da função .
Ver solução completaQuestão 343
8. Encontre a distância vertical máxima entre a reta e a parábola , para .
Ver solução completaQuestão 344
Às horas da manhã, um navio encontra-se a a leste de outro navio . O navio navega rumo oeste a , enquanto navega rumo sul a . Considerando que os navios mantenham essas direções, determine a menor distância entre os navios e quando essa distância ocorrerá.
Ver solução completaQuestão 345
Um dos lados de um campo retangular é limitado por um trecho de rio em linha reta. Deseja-se
cercar o campo com um fio de comprimento . Determine as dimensões do campo sabendo que a área é a maior possível.
Ver solução completaQuestão 346
Determine os pontos da curva mais próximos do ponto . Calcule a distância mínima.
Ver solução completaQuestão 355
1.1. Esboce a região e determine o máximo e o mínimo absolutos da função quando
b. e ;
Ver solução completaQuestão 356
1.1. Esboce a região e determine o máximo e o mínimo absolutos da função quando
c. e ;
Ver solução completaQuestão 357
1.1. Esboce a região e determine o máximo e o mínimo absolutos da função quando
d. e .
Ver solução completaQuestão 358
1.4. Encontre os pontos de máximo e de mínimo de em , sem parametrizar , quando
b. e ;
Ver solução completaQuestão 359
1.4. Encontre os pontos de máximo e de mínimo de em , sem parametrizar , quando
d. e ;
Ver solução completaQuestão 363
1.2. Determine o valor máximo e o valor mínimo da função sujeita às restrições explicitadas:
a. , sujeito a ;
Ver solução completaQuestão 364
1.3. Determine o valor máximo e o valor mínimo de na região sendo
a. e ;
Ver solução completaQuestão 365
1.3. Determine o valor máximo e o valor mínimo de na região sendo
b. e ;
Ver solução completaQuestão 366
1.4. Encontre os pontos de máximo e de mínimo de em , sem parametrizar , quando
a. e ;
Ver solução completaQuestão 367
1.4. Encontre os pontos de máximo e de mínimo de em , sem parametrizar , quando
c. e ;
Ver solução completaQuestão 369
1.2. Determine o valor máximo e o valor mínimo da função sujeita às restrições explicitadas:
b. , sujeito a ;
Ver solução completaQuestão 370
1.2. Determine o valor máximo e o valor mínimo da função sujeita às restrições explicitadas:
c. , sujeito a ;
Ver solução completaQuestão 379
Seja derivável e com um único ponto crítico . Prove que se for ponto de mínimo (máximo) local de , então será o único ponto de mínimo(máximo) global de .
Ver solução completaQuestão 380
7.25. Seja , , onde . Ache o menor valor de para o qual tem-se , para todo
Ver solução completaQuestão 385
Seja
- Encontre, caso exista, os máximos e mínimos (local e absoluto) de f.
- Determine os valores máximos e mínimo de em . Em que pontos esses valores são atingidos?
Questão 386
Obtenha os intervalos onde a função é côncava para cima ou para baixo
Ver solução completaQuestão 387
Seja
- Encontre, caso exista, os máximos e mínimos (local e absoluto) de f.
- Determine os valores máximos e mínimo de em . Em que pontos esses valores são atingidos?
Questão 388
Obtenha os intervalos onde a função é côncava para cima ou para baixo
Ver solução completaQuestão 389
Obtenha os intervalos onde a função é côncava para cima ou para baixo
Ver solução completaQuestão 390
1.1. Esboce a região e determine o máximo e o mínimo absolutos da função quando
a. e é o triângulo (com interior e lados inclusos) cujos vértices são , e ;
Ver solução completaQuestão 391
Determine os pontos de máximos e mínimos (Local e Global) das funções:
Questão 392
Obtenha os intervalos onde a função é côncava para cima ou para baixo
Ver solução completaQuestão 393
Que valor de faz ter:
- Um mínimo local em ?
- Um ponto de inflexão quando
Questão 394
Quais valores de fazem ter
- Um máximo local em e um mínimo local em
- Um mínimo local em e ponto de inflexão em
Questão 404
Considere a função:
Determine os intervalos de crescimento e decrescimento de , seus intervalos de concavidade, e classifique os seus pontos críticos como máximo local, mínimo local, ou sela (obs: nāo precisa achar uma fórmula para ).
Ver solução completaQuestão 405
7.23. Determine, caso exista, a constante a para que tenha
b. um ponto de mínimo local em .
Mostre ainda que, para qualquer valor de , a função não terá um ponto de máximo local.
Ver solução completaQuestão 406
7.28. Para que pontos da circunferência a soma das distâncias a e é mínima?
Ver solução completaQuestão 407
7.23. Determine, caso exista, a constante a para que tenha
a. um ponto de mínimo local em .
Ver solução completaQuestão 408
Seja . O ponto é ponto de
a. maximo local mas nao global.
b. minimo local mas nao global.
c. maximo global.
d. minimo global.
e. inflexao.
Ver solução completaQuestão 409
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
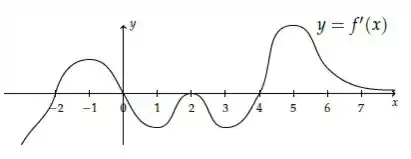
- Para que valores tem um máximo ou mínimo local?
Questão 410
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades
Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.
Ver solução completaQuestão 411
A taxa aeróbica de uma pessoa com anos de idade pode ser modelada pela seguinte função:
Quando . Em que idade uma pessoa tem capacidade aeróbica máxima?
Ver solução completaQuestão 413
Use os gráficos abaixo para dizer quais são os pontos e os valores de máximo e mínimo locais e globais da função.
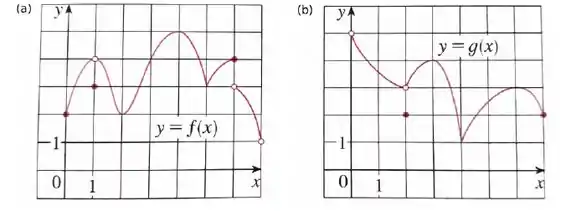
Questão 414
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(b)
Ver solução completaQuestão 415
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(c)
Ver solução completaQuestão 416
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(d)
Ver solução completaQuestão 417
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(e)
Ver solução completaQuestão 418
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(a)
Ver solução completaQuestão 419
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(f)
Ver solução completaQuestão 420
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(g)
Ver solução completaQuestão 421
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(h)
Ver solução completaQuestão 422
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(i)
Ver solução completaQuestão 423
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(j)
Ver solução completaQuestão 424
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(a) ,
Ver solução completaQuestão 425
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(b) ,
Ver solução completaQuestão 426
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(c) ,
Ver solução completaQuestão 427
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(g) ,
Ver solução completaQuestão 428
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(d) ,
Ver solução completaQuestão 429
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(e) ,
Ver solução completaQuestão 430
Em cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(f) ,
Ver solução completaQuestão 431
Após o consumo de uma bebida alcoólica, a concentração de álcool no sangue (CAS) aumenta rapidamente à medida que o álcool é absorvido, seguida por uma diminuição gradual conforme o álcool é metabolizado pelo fígado. A função
modela a CAS média, medida em mg/mL, de um grupo de oito indivíduos do sexo masculino horas depois do consumo rápido de de etanol (correspondendo a uma dose de bebida alcoólica). Qual é a CAS média máxima durantes as primeiras horas? Quando ela ocorre?
Ver solução completaQuestão 432
Determine as dimensões do paralelepípedo de volume máximo, com faces paralelas aos planos coordenados, de modo que uma das faces está contida no plano z = 0 e a correspondente face oposta tem os seus vértices no paraboloide .
Ver solução completaQuestão 433
Dentre todos os planos que são tangentes à superfície encontre aqueles mais distantes da origem.
Ver solução completaQuestão 434
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(c)
Ver solução completaQuestão 435
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(d)
Ver solução completaQuestão 436
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(e)
Ver solução completaQuestão 437
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(f)
Ver solução completaQuestão 438
Determine a equação do plano que passa por (2, 2, 1) e que delimita no primeiro octante o tetraedro de menor volume.
Ver solução completaQuestão 439
Calcule os pontos de máximo e de mínimo relativos (se existirem) de:
(h)
Ver solução completaQuestão 440
Um balão esférico perde ar por um furo de tal forma que seu raio diminui a uma taxa de . Qual a taxa de diminuição do volume, quando o raio do balão é ?
Ver solução completaQuestão 441
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(a)
Ver solução completaQuestão 442
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(g)
Ver solução completaQuestão 443
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(h)
Ver solução completaQuestão 444
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(c)
Ver solução completaQuestão 445
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(d)
Ver solução completa