Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.6 - Ex. 4

Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada segunda para encontrar os pontos de inflexão do gráfico da função e determine onde o gráfico é côncavo para cima e onde é côncavo para baixo. Faça um esboço do gráfico.

Passo 1

Para começar precisamos determinar quais são os pontos críticos da função. Esses pontos são os valores de x para os quais é igual a 0 ou para os quais não existe. Já para achar os pontos de inflexão do gráfico, ou seja, o ponto onde a função muda a direção da concavidade, precisamos achar os valores de x para os quais seja igual a 0 ou para os quais não existe.

Derivando a função:

Achando os pontos críticos:

Para achar os pontos de inflexão, a derivada segunda deve ser igual a 0:

Passo 2

Usando o teste da derivada segunda:

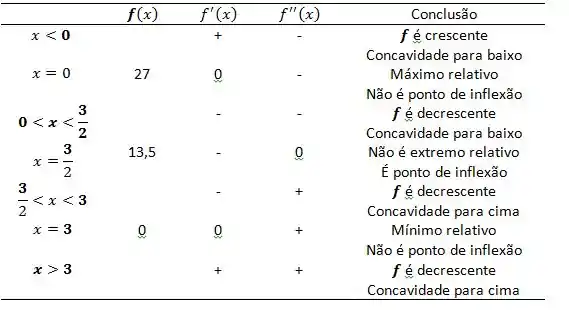
Pela tabela, podemos ver que , ou seja, temos um valor máximo e mínimo relativo, respectivamente. A mesma conclusão pode ser observada analisando a derivada primeira, o gráfico está crescendo para valores menores que e decrescendo para valores entre (), ou seja, ponto máximo. Para () a função decresce e cresce para valores maiores que , ou seja, ponto mínimo. Para o ponto de inflexão, a derivada segunda no intervalo () é negativa, concavidade para baixo, e positiva para , concavidade para cima, indicando que é um ponto de inflexão.

Desenhando o gráfico da função:

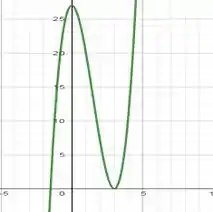
Resposta

Mínimo Relativo:

Máximo Relativo:

Pontos de inflexão;

O gráfico possui concavidade para cima para:

O gráfico possui concavidade para baixo para:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .d) f tem infinitos extremos relativos e f x → 0 quando x → + ∞ e x → - ∞ .

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .c) A função f tem exatamente dois extremos relativos no intervalo I e f x → + ∞ quando x → +

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .d) A função f tem exatamente dois extremos relativos no intervalo I e f x → - ∞ quando x → +

2. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .a) f tem exatamente um extremo relativo em I e f x → 0 quando x → + ∞ e x → - ∞ .

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .b) f é côncava para cima no intervalo I e não tem extremos relativos.