Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 1
O gráfico de uma função está na figura abaixo. Esboce os gráficos das seguintes equações:
(a)
(b)
(c)
(d)
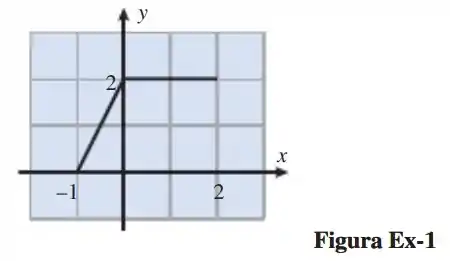
Passo 1
Bem, nessa questão, nós vamos usar os princípios de translação, alongamento, compreensão e reflexão vistos nesse capítulo e que ficaram bem resumidos na tabela 0.2.2, 0.2.3 e 0.2.4.
Basicamente:
Se temos uma função, por exemplo, e somamos uma constante positiva à função, por exemplo , deslocamos o gráfico da função na quantidade equivalente ao valor da constante para cima (no nosso exemplo, deslocaríamos em 1 unidade para cima no eixo ).
Se subtraímos uma constante à função (), deslocamos o gráfico para baixo (no exemplo, seria 1 unidade para baixo no eixo ).
Se somamos uma constante positiva ao (ex.:), deslocamos o gráfico para a esquerda (no exemplo, seria 1 unidade para a esquerda no eixo ).
Se subtraímos uma constante positiva ao (ex.:), deslocamos o gráfico para a direita (no exemplo, seria 1 unidade para a direita no eixo ).
Se multiplicamos a função por uma constante positiva maior que , alongamos o gráfico no eixo vertical por um fator equivalente à constante.
Se multiplicamos a função por uma constante positiva entre e , comprimimos o gráfico no eixo vertical por um fator equivalente à constante.
Se multiplicamos por uma constante positiva maior que , comprimimos o gráfico no eixo horizontal por um fator equivalente à constante.
Se multiplicamos por uma constante positiva entre e , alongamos o gráfico no eixo horizontal por um fator equivalente à constante.
Se substituímos por , refletimos o gráfico pelo eixo .
Se multiplicarmos a função por , refletimos o gráfico pelo eixo .
Vamos usar esses conceitos para resolver essa questão!! Onde temos uma com gráfico:
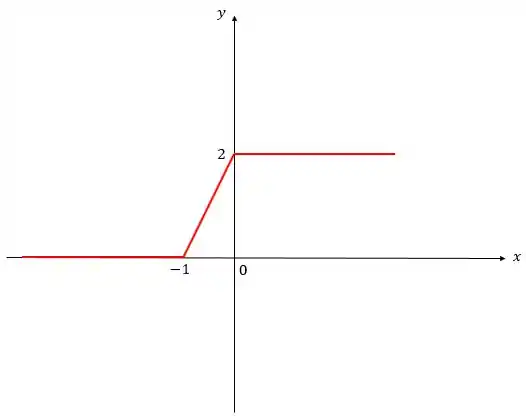
Obs.: sim sim, eu sei que essas linhas horizontais vermelhas se extendem pelo inteiro, mas eu decidi deixar elas cortadas para ficar mais fácil a visualização (fora que o problema não deixa nada explícito sobre isso né rs)! Para os curiosos, essa função é:
Maaass o intuito desse problema não é usar a definição da função, então vamos seguir! Essa foi apenas uma curiosidade.
Passo 2
(a) Se agora temos , estamos subtraindo uma constante positiva () da função! E, pela ideia do passo 1, vamos deslocar o gráfico por 1 unidade para baixo:
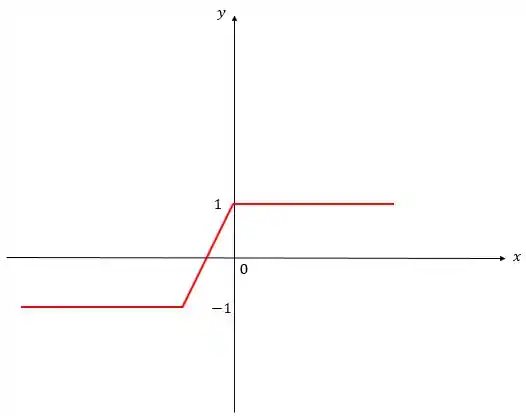
Passo 3
(b) Se agora temos , estamos subtraindo uma constante positiva () de ! E, pela ideia do passo 1, vamos deslocar o gráfico por 1 unidade para a direita:
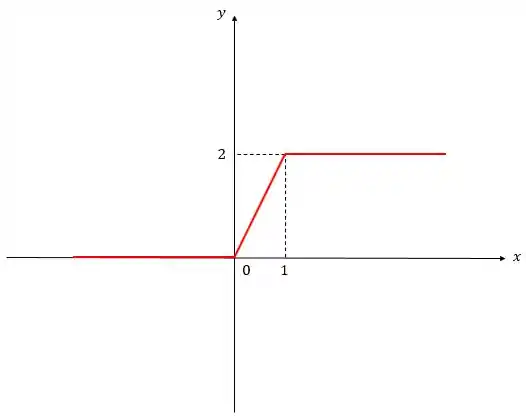
Passo 4
(c) Se agora temos , estamos multiplicando a função por uma constante positiva entre e ()! E, pela ideia do passo 1, vamos comprimir o gráfico pela metade ( unidade) no eixo :
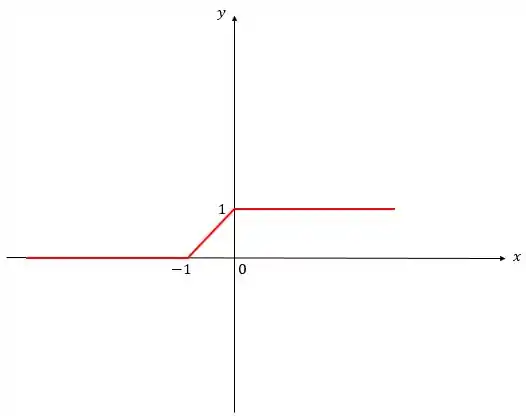
Obs.: Para saber que a função iria para o , é só fazer , pois comprimimos a função em um fator de no , como tínhamos um valor de no , ele cai pela metade (1).
Passo 5
(d) Se agora temos , estamos substituindo por , o que nos daria uma reflexão pelo eixo :
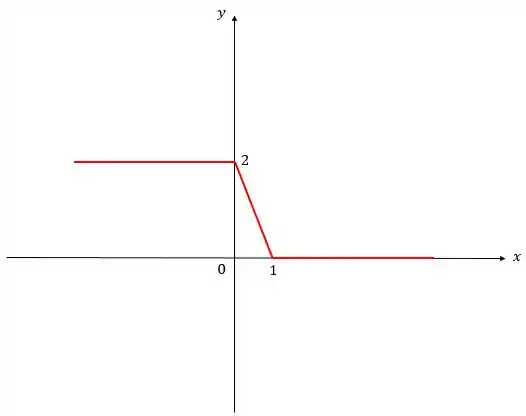
E, depois, multiplicando por uma constante positiva entre e ()! E, pela ideia do passo 1, vamos alongar o gráfico por (meia) unidade no eixo :
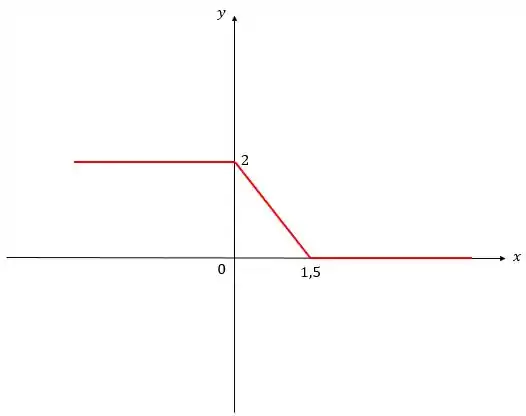
No final, ficou assim!
Resposta
Ei, a resposta está no passo a passo :)