Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.5 - Ex. 12
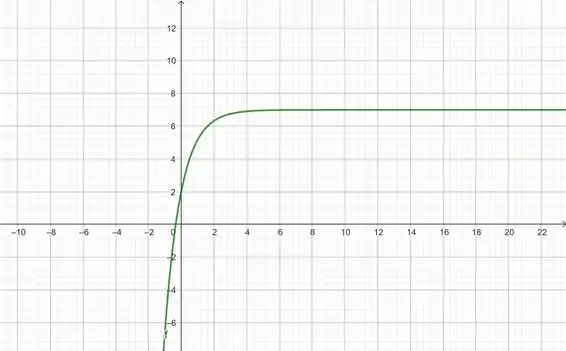
Faça um esboço do gráfico da função. Não use calculadora. Utilize somente os gráficos dados nas figuras e e, se necessário as transformações da seção
Passo 1
Desejamos fazer um esboço do gráfico da função dada no enunciado, para isso, vamos primeiro analisar as figuras e :
Aqui a gente tem a figura :
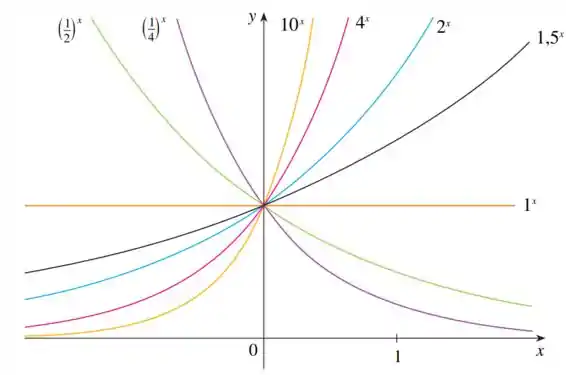
Onde a gente tem vários gráficos, mostrando como eles se comportam.
E aqui a gente tem a Figura 14:
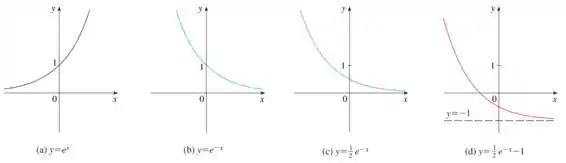
Então o que a gente vai fazer é utilizar desses gráficos, e dos nossos conhecimentos do comportamento dos gráficos das funções, quando uma operação com a função padrão é realizada por meio de uma ou mais constantes.
Passo 2
Então, para darmos início a nossa resolução vamos primeiro desenvolver nossa função, para que possamos comparar com alguma função base:
Realizando a distributiva:
Temos então:
Utilizando a figura 3 que é o gráfico da função e é o gráfico:
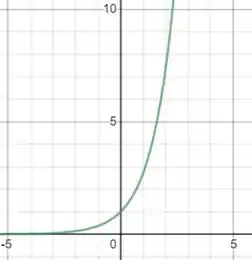
Iremos modificar esse gráfico com base no que as constantes fazem com o comportamento do gráfico de uma função, e assim iremos conseguir o gráfico da função:
Passo 3
Vemos que o gráfico que desejamos esboçar tem um que é o gráfico da figura espelhado em relação ao eixo dado por
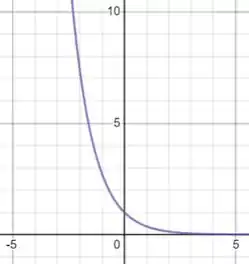
ele ainda está multiplicado por , ou seja, o ponto de corte em relação ao eixo vai ser o 5. Pois:
Assim, teremos
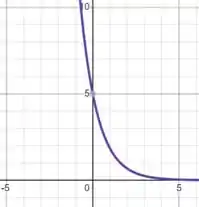
Passo 4
No entanto, também temos que o nosso gráfico é multiplicado por :
Isso significa que ele sofrerá uma rotação no eixo :
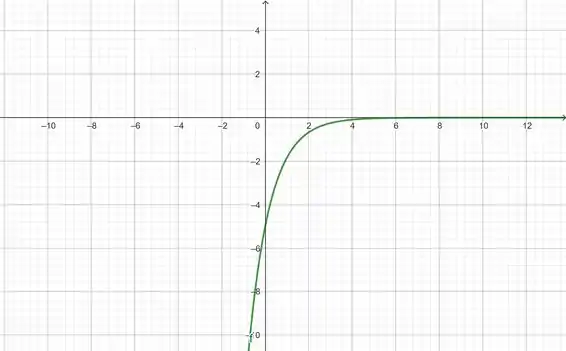
O último passo para a nossa resolução é a soma de unidades ao nosso gráfico. A soma ao gráfico de uma função faz com o que o mesmo se desloque unidades para cima no eixo , no nosso caso, unidades para cima:
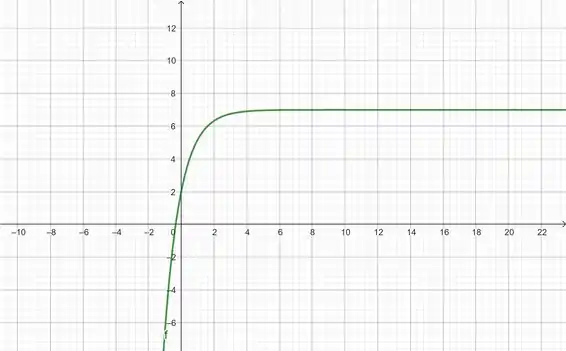
Resposta
