Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 29
Neste exercício, consideramos a família de funções , onde é um inteiro positivo.
a) Faça os gráficos das funções , e , na mesma tela usando a janela retangular por .
b) Faça os gráficos das funções , e na mesma tela usando a janela retangular por .
c) Faça os gráficos das funções , , e na mesma tela usando a janela retangular por .
d) Que conclusões você pode tirar desses gráficos?
Passo 1
Nessa questão vamos trabalhar com a função raíz tanto as de ordem par, quanto as de ordem ímpar.
Para ver como a função se comporta, vamos plotar e avaliar o gráfico para janelas gráficas dadas, isso é, vamos olhar o gráfico para o intervalo de valores de e estipulados em cada uma das letras.
Por fim, concluir o que essa análise vai nos trazer de resultado.
Passo 2
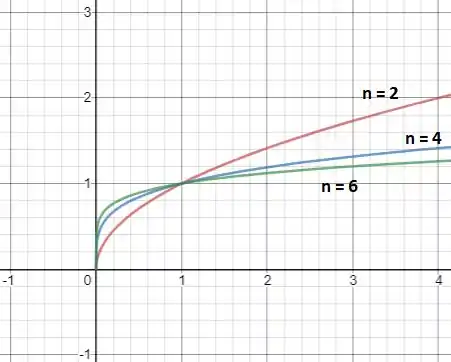
No item (a) devemos esboçar o gráficos das funções , e na janela por :
Passo 3
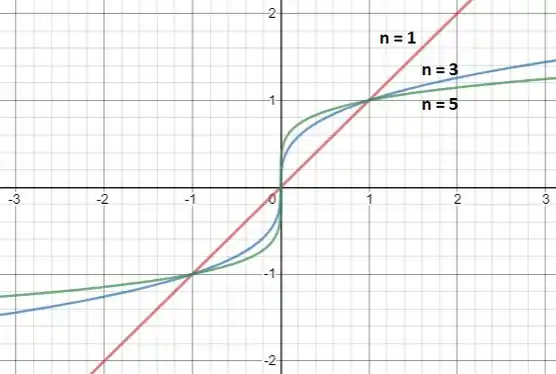
No item (b), devemos plotar as funções com , e na janela por :
Passo 4
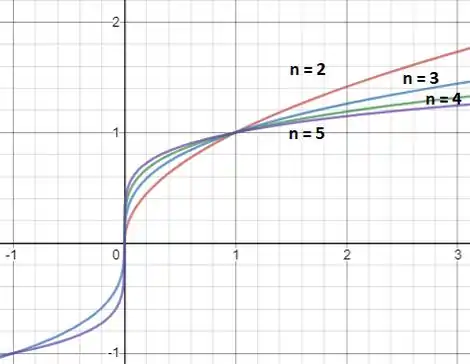
Já no item (c), considerando a janela pedida:
Passo 5
Item d)
Vemos que para par, apenas a parte é importante, ou seja a função tem como domínio valores de maiores ou igual a zero.
Enquanto para ímpar é importante a parte positiva e a parte negativa do eixo , dessa forma, a função tem como domínio qualquer valor de .
Para valores de entre e , a função cresce mais quando é maior.
Já para valores de maiores que , a função cresce mais quando é menor.
Resposta
Esboço de gráfico.