Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 24
Vimos, no exemplo 9, que a equação tem exatamente uma solução.
a) Use um gráfico para mostrar que a equação tem três soluções e encontre-as com duas casas decimais de precisão.
b) Encontre um valor aproximado tal que a equação tenha exatamente duas soluções.
Passo 1
Oie, tudo bem? Vamos resolver essa atividade aqui.
Queremos achar as soluções da equação graficamente.
Para isso, plotamos as funções e e olhamos para seus pontos de encontro, iremos utilizar o GeoGebra, mas veja que você pode plotar esse gráfico utilizando o desmos ou outro software que você goste.
Passo 2
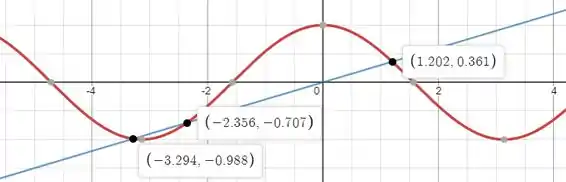
Assim, as soluções são:
Passo 3
Plotando os gráficos de , e em uma mesma tela,
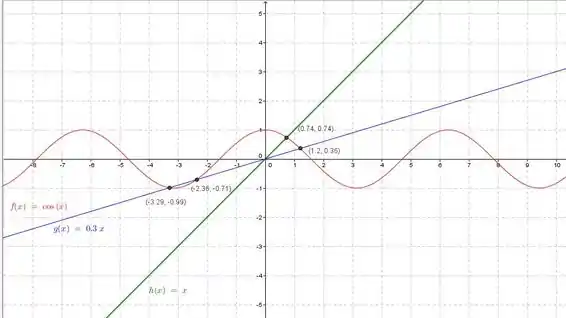
Precisamos encontrar a inclinação de para que haja apenas dois pontos de interseção.
No gráfico, podemos ver que, para ter apenas dois pontos de interseção, a nova linha deve ser mais íngreme que o gráfico de mas menos íngreme que o gráfico de → .
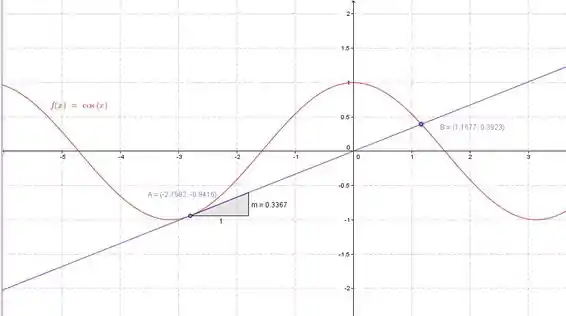
No gráfico, podemos ver que a única maneira de ter apenas dois pontos de interseção é que a linha azul seja tangente à curva no lado esquerdo e a cruze no lado direito. Portanto, precisamos tentar com diferentes valores de no intervalo dado, com valores mais próximos de do que de .
Usando a ferramenta de programa do CAS ou da calculadora, você pode encontrar a linha tangente que vai do ponto A até a origem , intersectando a curva no ponto B, e encontrar a inclinação correspondente .
Os dois pontos de interseção são:
