Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 2
O gráfico de é mostrado.
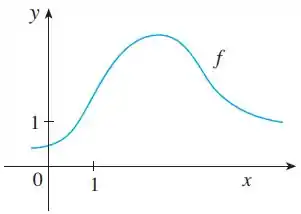
(a) Explique por que a série
não é a série de Taylor de centrada em .
(b) Explique por que a série
não é a série de Taylor de centrada em .
Passo 1
E aí, amigos! Tudo tranquilo?
A questão traz para nós um gráfico de uma função mas não traz exatamente qual função seria essa, somente sua curva e alguns pontos de e .
Na letra a) e na letra b) a questão quer saber porque a série em questão não é a série de Taylor centrada em um valor .
Olhando a curva, o que podemos ver é seu comportamento, ou seja, onde ela cresce ou decresce. Essa característica da função é dada pela primeira derivada, lembra?
Também podemos usar o sinal da segunda derivada, que vai dizer como será a concavidade da curva.
Acontece que os termos das séries de Taylor trazem essas derivadas, pois são da forma:
Então para cada série vamos analisar o sinal de suas derivadas.
Bora!
Passo 2
(a) Nossa série é:
No ponto podemos observar que a função está crescente, portanto, sua primeira derivada deve ser positiva. Como temos um formato de série de Taylor, o coeficiente que acompanha uma potência de , carrega o sinal da -ésima derivada, já que no formato de Taylor
podemos ver que o fatorial é sempre positivo então se olharmos para a série que foi dada, no segundo termo , temos um termo negativo, o que implica na primeira derivada negativa, o que não condiz com a função do gráfico.
Passo 3
(b) Nossa série é:
Para a segunda série dada, temos que o segundo termo , temos um sinal positivo, que para a segunda derivada representa uma concavidade positiva, mas no gráfico podemos observar que temos uma concavidade negativa, então a série não condiz com a função do gráfico.
Resposta
Afirmações a) e b) explicadas.