Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 73
Como os gráficos e estão relacionados ao gráfico ? Em geral, como o gráfico de está relacionado ao gráfico de ?
Passo 1
Essa questão pede para que façamos uma análise gráfica comparando funções com o deslocado, e que façamos uma conclusão geral para uma função genérica.
Para isso, vamos usar uma ferramenta gráfica para desenhar os gráficos e analisarmos.
Passo 2
Gráficos das funções:
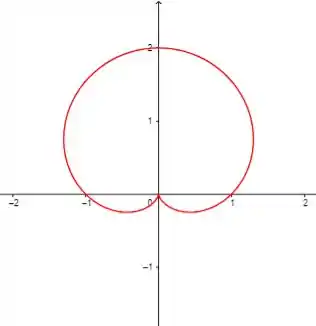
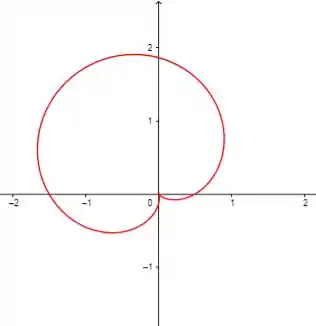
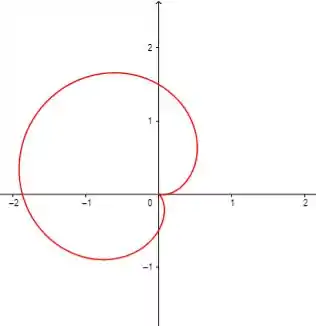
Pela análise dos gráficos de , sendo um ângulo qualquer, podemos dizer que este gráfico é apenas o gráfico de rotacionado no sentido anti-horário por este ângulo .
Passo 3
Utilizando o gráfico de relacionado ao gráfico de exemplo, podemos concluir que o gráfico de é o gráfico de rotacionado um ângulo .
Resposta
O gráfico de é o gráfico de rotacionado um ângulo .
Exercícios de Livros Relacionados
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 1 + sen θ
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 2 + sen θ
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r 2 = cos θ
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r 2 = - cos θ
Desenhe as lemniscatas nos Exercícios 13-16. Quais simetrias essas curvas têm? r 2 = 4 sen 2 θ