Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 7
Determine os sinais das derivadas parciais da função cujo gráfico está mostrado.
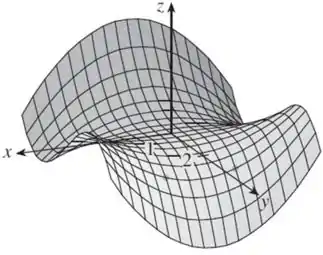
(a)(b)
Passo 1
Fala, galera! Beleza?
Nessa questão nós temos o gráfico de uma função e queremos saber o sinal da derivada segunda em um certo ponto. Em particular, nesse item a), nós temos que determinar o sinal da derivada parcial de com relação a e no ponto
Para isso, no item a), vamos fixar e olhar o ponto e pedido, analisando somente a concavidade da função no plano .
Depois, no item b), vamos fixar e olhar o ponto e pedido, analisando somente a concavidade da função no plano .
Vem comigo que eu te explico!
Passo 2
Para responder o item a), vamos observar o ponto
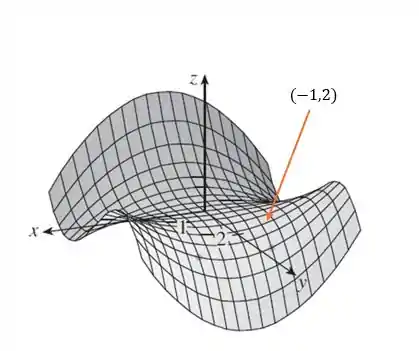
Podemos ver que, analisando , o gráfico da função no plano terá concavidade para cima no ponto .
Logo, podemos dizer que a derivada segunda da função é positiva nesse ponto, isto é, é positivo.
Passo 3
Para responder ao item b), vamos observar o gráfico da função no passo anterior.
Nós conseguimos ver que, no ponto , para , o gráfico da função tem concavidade para baixo, ou seja, a derivada segunda é negativa nesse ponto.
Logo,
Agora, é negativo.