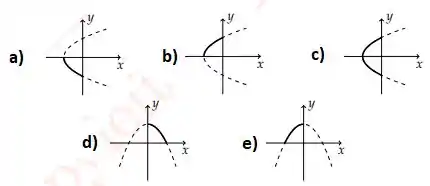Exercícios de Esboço de Curvas - Lista de Exercícios Resolvida
Questão 1
Seja a curva parametrizada:
Faça um esboço da trajetória percorrida pela partícula.
Ver solução completaQuestão 3
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine sua equação cartesiana:
a) , ,
c) , ,
f) , ,
Ver solução completaQuestão 4
Seja a curva parametrizada:
Faça um esboço da trajetória percorrida pela partícula.
Ver solução completaQuestão 5
Seja uma partícula cuja posição no espaço ao longo do tempo é descrita pela função vetorial , com .
Faça um esboço da trajetória percorrida pela partícula.
Ver solução completaQuestão 10
Considere a curva definida pela função vetorial
onde .
Mostre que a curva está contida em uma superfície quádrica. Identifique essa superfície e use esse fato para esboçar a curva .
Ver solução completaQuestão 11
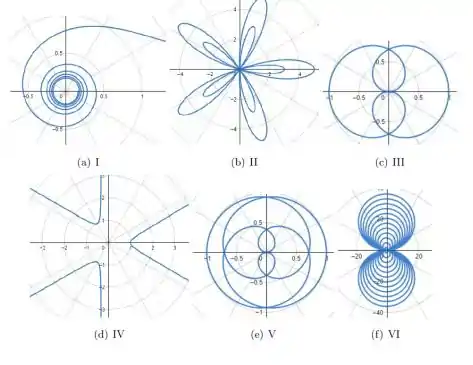
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 12
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 14
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 15
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 16
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 18
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 22
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Ver solução completaQuestão 23
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Ver solução completaQuestão 26
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Ver solução completaQuestão 28
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Ver solução completaQuestão 29
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Ver solução completaQuestão 32
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
.
Ver solução completaQuestão 33
A função é definida como
Calcule e
Qual é o domínio desta função?
Verifique que esta função é ímpar.
Faça o gráfico. Sugestão. Faça o gráfico de e e utilize a subtração de gráficos.
Ver solução completaQuestão 34
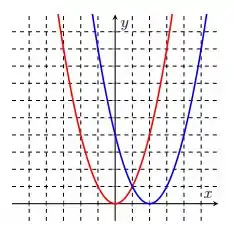
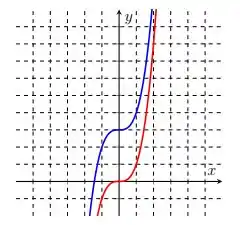
Nos itens abaixo, o gráfico da função está em vermelho e o da função em azul. Encontre a regra de formação de a partir de .
.
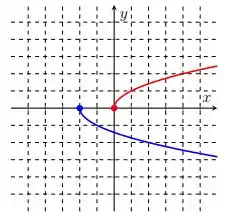
.
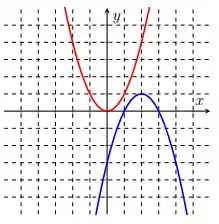
Questão 36
Seu professor de matemática pediu para fazer o gráfico da função para de a usando uma escala de unidades para cada centímetro da folha. Quais são as dimensões da folha necessária para o gráfico?
Ver solução completaQuestão 37
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
Ver solução completaQuestão 38
Use o gráfico da função para desenhar o gráfico das funções abaixo.
.
.
Ver solução completaQuestão 39
Considere a função cujo gráfico está no enunciado do exercício anterior. Observe que, próximo ao ponto , todos os valores de são menores ou iguais a . Nesse caso, dizemos que é um máximo local para . Da mesma forma, também é um máximo local. Com um raciocínio análogo, dizemos que e são mínimos locais. Outra forma de expressar é dizer que possui máximos locais em e e mínimos locais em e . Nos itens abaixo, determine os máximos e mínimos locais, assim como os valores de nos quais são atingidos.
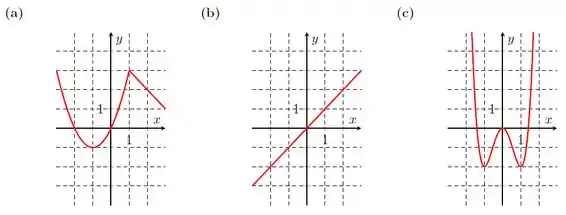
Questão 40
Determine quais funções são pares, quais são ímpares ou nehuma nem outra.
a)
b)
c)
d)
e)
f)
g)
h)
Ver solução completaQuestão 42
Nos itens abaixo, faça o gráfico da inversa da função cujo gráfico está representado.
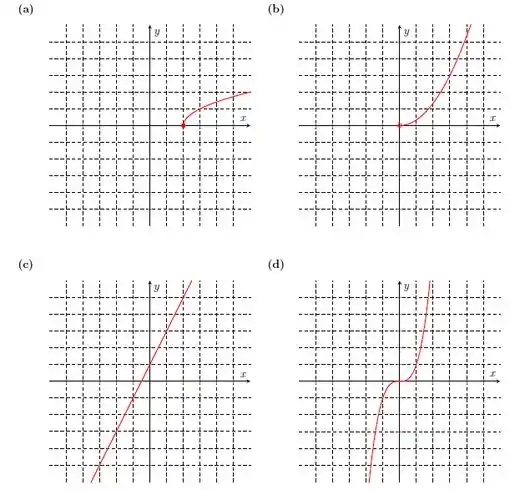
Questão 43
Nos itens abaixo, explique como obter o gráfico da função a partir do gráfico da função .
a) e
b) e
c) e
d) e
e) e
f) e
Ver solução completaQuestão 44
Seja uma função com domínio simétrico em relação à origem (por exemplo, um domínio da forma ). Dizemos que é uma função par se para todos . Se para todos , dizemos que é uma função ímpar. Por exemplo, é uma função par, pois para todo , . A função é uma função ímpar, pois para todo , . A função não é nem par nem ímpar, pois e essa expressão não é igual a para todo . O gráfico das funções pares possui a propriedade de ser simétrico em relação ao eixo das ordenadas (isto é, a metade esquerda e a metade direita do gráfico são espelhadas). O gráfico das funções ímpares possui a propriedade de ser simétrico em relação à origem (isto é, se o ponto pertence ao gráfico , então o ponto também pertence). Complete o gráfico da função em que uma parte do gráfico está desenhada abaixo, sabendo que:
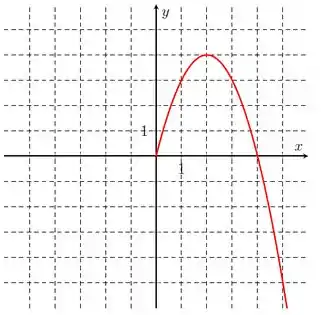
a) A função é par
b) A função é ímpar
Ver solução completaQuestão 45
Suponha que seja conhecido o gráfico de uma função . Em cada item, descreva como obter o gráfico da função a partir do gráfico da função .
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
n)
o)
p)
q)
r)
s)
t)
Ver solução completaQuestão 46
Em cada item, uma função é dada e uma sequência de operações é realizada sobre seu gráfico. Determine a regra de formação da função cujo gráfico é obtido após as operações.
; o gráfico é transladado unidades para cima.
; o gráfico é transladado unidade para baixo.
; o gráfico é transladado unidades para a esquerda.
; o gráfico é transladado unidade para a direita.
Ver solução completaQuestão 47
Nos itens abaixo, o gráfico da função está em vermelho e o da função em azul. Encontre a regra de formação de a partir de .
.
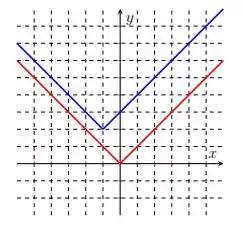
.
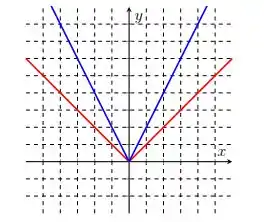
Questão 48
Em cada item, uma função é dada e uma sequência de operações é realizada sobre seu gráfico. Determine a regra de formação da função cujo gráfico é obtido após as operações.
o gráfico é esticado verticalmente por um fator , transladado unidades para baixo e para a direita.
o gráfico é encolhido verticalmente por um fator , transladado uma unidade para a esquerda e para cima.
o gráfico é refletido em relação à reta
Ver solução completaQuestão 49
Em cada item, uma função é dada e uma sequência de operações é realizada sobre seu gráfico. Determine a regra de formação da função cujo gráfico é obtido após as operações.
o gráfico é transladado unidades para a direita e para cima.
o gráfico é refletido em relação ao eixo e transladado unidade para cima.
o gráfico é transladado unidades para a esquerda e refletido em relação ao eixo .
Ver solução completaQuestão 50
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
.
Ver solução completaQuestão 51
Use o gráfico da função para desenhar o gráfico das funções abaixo.
.
.
Ver solução completaQuestão 52
Use o gráfico da função para desenhar o gráfico das funções abaixo.
a)
b)
c)
d)
Ver solução completaQuestão 53
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
Ver solução completaQuestão 58
Nos itens abaixo, o gráfico da função está em vermelho e o da função em azul. Encontre a regra de formação de a partir de .
Questão 60
Utilize o gráfico da função para fazer os gráficos das funções abaixo.
.
.
.
.
Ver solução completaQuestão 61
Faça o gráfico das funções abaixo montando uma tabela de valores. Se necessário, use uma calculadora.
Ver solução completaQuestão 63
Faça o gráfico das funções . Determine o domínio, a imagem, o período e a paridade de cada uma delas.
Ver solução completaQuestão 64
Faça o gráfico das funções abaixo montando uma tabela de valores. Se necessário, use uma calculadora.
.
.
Ver solução completaQuestão 70
Faça o gráfico das funções abaixo, determinando o período, a amplitude, a fase e a imagem.
Questão 76
a) Esboce a região
b) Efetuando uma mudança de variáveis apropriada, calcular a integral
Dica: considerar e determinar tal que a mudança de variáveis simplifique o domínio de integração.
Ver solução completaQuestão 77
Considere a curva parametrizada
(a) Esboce a curva e encontre seu comprimento.
(b) Encontre a posição do centroide da curva
Ver solução completaQuestão 78
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos:
Ver solução completaQuestão 79
Dada a curva definida por .
Esboce a curva e indique com setas a direção na qual o parâmetro cresce.
Ver solução completaQuestão 82
Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:
- é a parte da esfera interior ao cone ;
Questão 83
Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:
b) é a parte do cilindro compreendida entre os planos e ;
Ver solução completaQuestão 87
Considere a área da região de intersecção às curvas e .
Parte I) Esboce a região
Ver solução completaQuestão 89
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Represente (sem calcular!) a área de por uma ou mais integrais definidas em termos de .
Ver solução completaQuestão 90
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Esboce a região .
Ver solução completaQuestão 91
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Represente (sem calcular!) a área de por uma ou mais integrais definidas em termos de .
Ver solução completaQuestão 92
Uma curva polar consiste em todos os pontos que têm pelo menos uma representação cujas coordenadas satisfazem a equação. Por exemplo, a curva representada pela equação é um círculo de raio e centro na origem. A curva é uma reta que passa na origem com inclinação radiano. Desta forma, esboce a curva polar . Calcule a inclinação de sua reta tangente quando . Encontre todos os pontos onde a reta tangente é horizontal e vertical.
Ver solução completaQuestão 94
Faça o esboço do gráfico da função
destacando informações relacionadas a domínio, continuidade, derivabilidade, interseções com os eixos coordenados, assíntotas, pontos críticos, intervalos de crescimento e decrescimento, concavidade, pontos de inflexão e extremos locais ou absolutos.
Ver solução completaQuestão 97
A demanda de um certo produto é unidades por mês quando o preço é p reais a unidade.
(b) Expresse o gasto mensal total nesse produto em função de p. (O gasto mensal total é a quantia total que os consumidores gastam para adquirir um produto durante um mês.)
Ver solução completaQuestão 98
Esboce o gráfico de uma função que satisfaça todas as seguintes características:
é par
Ver solução completaQuestão 100
Esboce o gráfico de uma função com as seguintes características:
E se , então .
Ver solução completaQuestão 102
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas elementares e então aplicando as transformações apropriadas
Ver solução completaQuestão 103
Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
e .
Ver solução completaQuestão 104
Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
Ver solução completaQuestão 105
Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
e .
Ver solução completaQuestão 106
3. Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
(d) e .
Ver solução completaQuestão 107
1. Determine os zeros (caso existam) e o vértice das funções quadráticas seguintes. Em seguida, esboce seus gráficos:
(a)
Ver solução completaQuestão 108
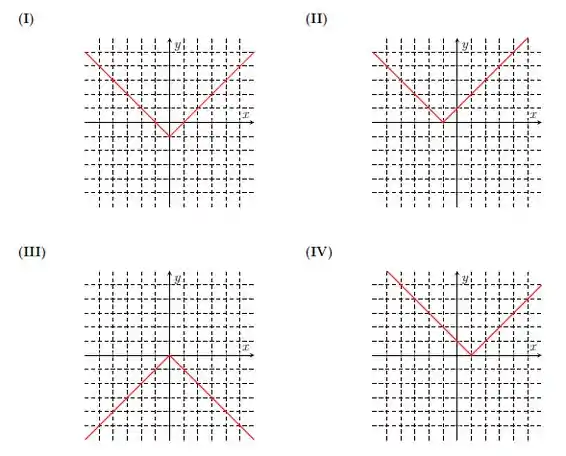
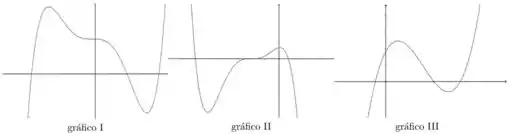
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico
(b) ;
Questão 109
Usando o conhecimento do gráfico de função , da identidade dado pelo produto notável e a noção de deslocamento horizontal, trace um esboço do gráfico das seguintes funções:
(a) .
Ver solução completaQuestão 110
1. Determine os zeros (caso existam) e o vértice das funções quadráticas seguintes. Em seguida, esboce seus gráficos:
(b)
Ver solução completaQuestão 111
Usando o conhecimento do gráfico de função , completamento de quadrados e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:
(a)
Ver solução completaQuestão 112
Usando o conhecimento do gráfico de função , completamento de quadrados e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:
(b)
Ver solução completaQuestão 113
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico
(a) ;
Questão 114
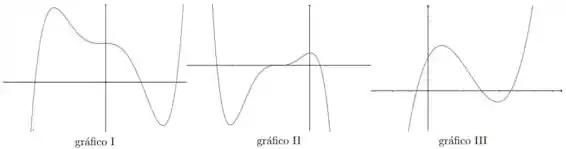
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico
(c) ;
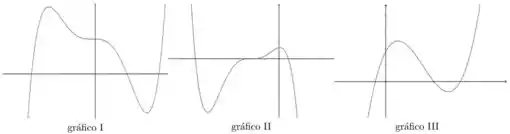
Questão 116
14. Esboce à mão o gráfico de e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de (nos domínios indicados).
a) ,
Ver solução completaQuestão 117
14. Esboce à mão o gráfico de e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de (nos domínios indicados).
b) ,
Ver solução completaQuestão 118
14. Esboce à mão o gráfico de e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de (nos domínios indicados).
c)
Ver solução completaQuestão 119
14. Esboce à mão o gráfico de e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de (nos domínios indicados).
d)
Ver solução completaQuestão 120
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Esboce o gráfico de
Ver solução completaQuestão 122
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Esboce o gráfico de .
Ver solução completaQuestão 123
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Esboce o gráfico de .
Ver solução completaQuestão 134
Na função a seguir calcule
Seus Intervalos de D onde f é crescente e onde f é decrescente.
Extremos relativos (locais) e absolutos (globais) de f.
Intervalos em que o gráfico de f é côncavo para cima, onde é côncavo para baixo e os seus
pontos de inflexão.
Ver solução completaQuestão 137
Considere a função , definida em seu maior domínio possível.
e) Faça um esboço do gráfico, utilizando todas as informações dos itens anteriores.
Ver solução completaQuestão 139
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
h) Esboce o gráfico de .
Ver solução completaQuestão 144
Faça o esboço do traço de cada curva parametrizada abaixo indicando a sua orientação:
(a)
Ver solução completaQuestão 145
Faça o esboço do traço de cada curva parametrizada abaixo indicando a sua orientação:
(b)
Ver solução completaQuestão 146
Faça o esboço do traço de cada curva parametrizada abaixo indicando a sua orientação:
(d)
Ver solução completaQuestão 147
A curva parametrizada por
Está contida em
- Um cone com vértice no ponto
- Um plano
- Uma efera com centro no ponto
- Um paraboloide
- Um cilindro
Questão 148
Usando o conhecimento do gráfico de função , da identidade dado pelo produto notável e a noção de deslocamento horizontal, trace um esboço do gráfico das seguintes funções:
(b) .
Ver solução completaQuestão 149
Faça um esboço do gráfico de cada uma das inversas das seguintes funções trigonométricas (primeiro verifique qual é o domínio e imagem a dessas funções!): f (x) = cos (x), g (x) = sen (x ) e h (x) = tag (x )
Ver solução completaQuestão 150
Esboce os gráficos das funções abaixo. Qual é o período de cada uma?
(b)
Ver solução completaQuestão 151
Encontre a forma Fase-Amplitude em termos de uma senoide e, também, em termos de uma cossenóide, das seguintes funções:
(b) ;
Ver solução completaQuestão 152
Para as funções cujas leis são dadas abaixo, verifique se são limitadas em seu domínio de definição. Caso não seja limitada, verifique por qual sequência de pontos ela cresce (ou decresce) arbitrariamente:
k)
Ver solução completaQuestão 158
2. O número de pessoas infectadas por uma epidemia de dengue é modelado por:
(a) Esboce o gráfico de .
Ver solução completaQuestão 165
Para a função , calcule e , determine e esboce o domínio e determine a imagem de .
Ver solução completaQuestão 169
Considere a função definida no intervalo .
Esboce os gráficos das suas extensões par e ímpar, de período , no intervalo .
Ver solução completaQuestão 170
18. Nos exercícios de a) - f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
a)
Ver solução completaQuestão 171
18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
b)
Ver solução completaQuestão 172
18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
d)
Ver solução completaQuestão 173
26. Faça o gráfico da função e em seguida, responda:
a) Qual é o domínio e a imagem de ?
Ver solução completaQuestão 174
18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
f)
Ver solução completaQuestão 175
26. Faça o gráfico da função e em seguida, responda:
b) Em quais pontos , se houver, existe?
Ver solução completaQuestão 177
Encontre a área da região sombreada na figura abaixo, a qual é delimitada pela curva e uma pétala de .
Ver solução completaQuestão 178
26. Faça o gráfico da função e em seguida, responda:
d) Em quais pontos existe o limite à direita?
Ver solução completaQuestão 179
26. Faça o gráfico da função e em seguida, responda:
c) Em quais pontos existe o limite à esquerda?
Ver solução completaQuestão 180
6 – Seja
d) Calcule , identifique o seu domínio e esboce seu gráfico.
Ver solução completaQuestão 181
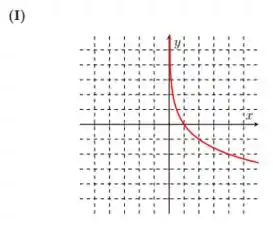
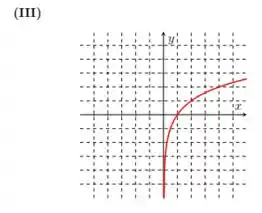
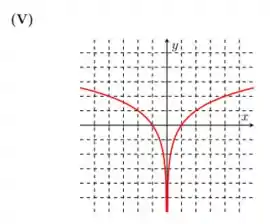
Esboçar o gráfico de para diferentes valores de , incluindo os valores e
I)
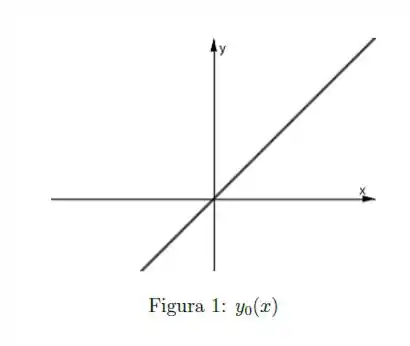
Questão 182
Esboce os gráficos das funções abaixo. Qual é o período de cada uma?
(d)
Ver solução completaQuestão 184
Considere funções:
E
Encontre as coordenadas dos pontos em que o gráfico da função corta os eixos coordenados.
Esboce o gráfico de . Explique a construção do gráfico da função , usando transformações em gráfico (translações, reflexões...) a partir do gráfico da função Descreva essas transformações em palavras.
Responda qual é o domínio da função .
Levando em consideração os gráficos obtidos nos itens anteriores e o gráfico da função , esboce o gráfico da função .
Responda qual é a imagem da função .
Observando o gráfico da função , dê os intervalos do domínio em que a função é decrescente. Esboce o gráfico da função e da função . Explique a construção desses gráficos.
A função é par? É ímpar? Nem uma coisa e nem outra? Explique!
A função é par? É ímpar? Nem uma coisa e nem outra? Explique!
Ver solução completaQuestão 185
1. Durante uma epidemia de dengue, o número de pessoas que adoeceram, num certo bairro, após dias é dado por:
(b) Esboce o gráfico de
Ver solução completaQuestão 186
Considere a parábola definida pela função quadrática . Complete o quadrado na variável x e escreva a função quadrática na forma canônica.
“Lembre que a forma canônica de uma função quadrática é , onde são constantes reais.”
A partir dessa forma canônica encontre o vértice dessa parábola. Justifique sua resposta! A questão só será pontuada se o vértice for encontrado e justificado através da forma canônica. Responda qual é a concavidade dessa parábola. Justifique!
Encontre os pontos de interseção dessa parábola com os eixos coordenados, quando existirem. Deixe os cálculos para justificar sua resposta.
Esboce o gráfico da função , marcando no gráfico o vértice e os pontos de interseção que existirem.
Ver solução completaQuestão 188
Esboce os gráficos das funções abaixo. Qual é o período de cada uma?
(c)
Ver solução completaQuestão 190
Considere a curva definida pela função vetorial
onde .
Mostre que a curva está contida em uma superfície quádrica. Identifique essa superfície e use esse fato para esboçar a curva .
Ver solução completaQuestão 191
A demanda de um certo produto é unidades por mês quando o preço é p reais a unidade.
(c) Faça um gráfico da função de gasto mensal total.
Ver solução completaQuestão 192
A demanda de um certo produto é unidades por mês quando o preço é p reais a unidade.
(e) Use o gráfico do item (c) para estimar o preço para o qual o gasto mensal é máximo.
Ver solução completaQuestão 193
Esboce os gráficos das funções abaixo. Qual é o período de cada uma?
Questão 194
Faça o esboço do traço de cada curva parametrizada abaixo indicando a sua orientação:
(e)
Ver solução completaQuestão 195
Para cada item abaixo, encontre pelo menos duas funções a valores vetoriais e distintas satisfazendo a equação dada. (Conclui-se, assim, que uma parametrização de uma curva não é única.)
(a)
Ver solução completaQuestão 196
Para cada item abaixo, encontre pelo menos duas funções a valores vetoriais e distintas satisfazendo a equação dada. (Conclui-se, assim, que uma parametrização de uma curva não é única.)
(c)
Ver solução completaQuestão 197
Encontre a forma Fase-Amplitude em termos de uma senoide e, também, em termos de uma cossenóide, das seguintes funções:
(a) ;
Ver solução completaQuestão 200
Considere as funções e .
O gráfico da função é parte de uma curva conhecida. Esboce o seu gráfico e explique a construção desse gráfico identificando a curva que dá origem a ele. Justifique!
A partir do gráfico da função explique como é possível construir o gráfico da função usando três transformações em gráfico (translações, reflexões...). Descreva essas transformações em palavras. Esboce o gráfico da função .
Ver solução completaQuestão 201
A curva parametrizada por
Está contida em:
- Um plano
- Um paraboloide
- Um cone
- Um hiperboloide
- Um elipsoide
Questão 208
A demanda de um certo produto é unidades por mês quando o preço é p reais a unidade.
(a) Faça um gráfico dessa função de demanda.
Ver solução completaQuestão 210
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
a. ;
Ver solução completaQuestão 211
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráfico, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
b)
Ver solução completaQuestão 212
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráco, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
c)
Ver solução completaQuestão 213
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráfico, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
d)
Ver solução completaQuestão 214
Considere as seguintes afirmações:
- A imagem da curva está contida em uma reta.
- A imagem da curva é uma parábola.
- A imagem da curva está contida em uma hipérbole.
São corretas apenas as afirmações:
Questão 215
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráfico, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
f)
Ver solução completaQuestão 216
Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
Ver solução completaQuestão 218
Use um recurso gráfico para comparar a função exponencial , e a função potência . Qual função crescerá mais rapidamente para valores de grande?
Ver solução completaQuestão 220
Na função a seguir calcule
Seu domínio, sua paridade, e as assíntotas verticais e horizontais
Ver solução completaQuestão 221
Na função a seguir calcule
Seu domínio, sua paridade, e as assíntotas verticais e horizontais
Ver solução completaQuestão 222
Na função a seguir calcule
Seus Intervalos de D onde f é crescente e onde f é decrescente.
Extremos relativos (locais) e absolutos (globais) de f.
Intervalos em que o gráfico de f é côncavo para cima, onde é côncavo para baixo e os seus
pontos de inflexão.
Ver solução completaQuestão 223
Na função a seguir calcule
Seus Intervalos de D onde f é crescente e onde f é decrescente.
Extremos relativos (locais) e absolutos (globais) de f.
Intervalos em que o gráfico de f é côncavo para cima, onde é côncavo para baixo e os seus
pontos de inflexão.
Ver solução completaQuestão 234
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
c. ;
Ver solução completaQuestão 235
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
h. ;
Ver solução completaQuestão 237
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
d. ;
Ver solução completaQuestão 238
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
j. ;
Ver solução completaQuestão 239
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
f. ;
Ver solução completaQuestão 241
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
b. ;
Ver solução completaQuestão 242
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
g. ;
Ver solução completaQuestão 244
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
e. ;
Ver solução completaQuestão 246
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
i. ;
Ver solução completaQuestão 255
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 257
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas elementares e então aplicando as transformações apropriadas
Ver solução completaQuestão 258
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas elementares e então aplicando as transformações apropriadas
Ver solução completaQuestão 260
Considere os vetores , e . Determine e represente graficamente:
c) A projeção escalar de sobre .
Ver solução completaQuestão 261
Considere os vetores , e . Determine e represente graficamente:
d) A projeção vetorial de sobre .
Ver solução completaQuestão 262
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo );
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
a)
Ver solução completaQuestão 263
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráfico, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
a)
Ver solução completaQuestão 264
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo y);
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
f)
Ver solução completaQuestão 265
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráfico, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
e)
Ver solução completaQuestão 266
4. Com base no domínio, contra-domínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função.
e)
Ver solução completaQuestão 267
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo y);
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
e)
Ver solução completaQuestão 268
4. Com base no domínio, contra-domínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função.
f)
Ver solução completaQuestão 269
4. Com base no domínio, contra-domínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função.
d)
Ver solução completaQuestão 270
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo y);
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
b)
Ver solução completaQuestão 271
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo y);
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
d)
Ver solução completaQuestão 272
4. Com base no domínio, contra-domínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função.
c)
Ver solução completaQuestão 273
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
a)
Ver solução completaQuestão 274
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
b)
Ver solução completaQuestão 275
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
c)
Ver solução completaQuestão 276
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
d)
Ver solução completaQuestão 277
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
e)
Ver solução completaQuestão 278
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
f)
Ver solução completaQuestão 279
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
g)
Ver solução completaQuestão 280
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
h)
Ver solução completaQuestão 281
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
i)
Ver solução completaQuestão 283
Na função a seguir calcule
Seu domínio, sua paridade, e as assíntotas verticais e horizontais
Ver solução completaQuestão 285
Na função a seguir calcule
Seu domínio, sua paridade, e as assíntotas verticais e horizontais
Ver solução completaQuestão 286
Na função a seguir calcule
Seus Intervalos de D onde f é crescente e onde f é decrescente.
Extremos relativos (locais) e absolutos (globais) de f.
Intervalos em que o gráfico de f é côncavo para cima, onde é côncavo para baixo e os seus
pontos de inflexão.
Ver solução completaQuestão 288
Na função a seguir calcule
Seu domínio, sua paridade, e as assíntotas verticais e horizontais
Ver solução completaQuestão 289
Na função a seguir calcule
Seus Intervalos de D onde f é crescente e onde f é decrescente.
Extremos relativos (locais) e absolutos (globais) de f.
Intervalos em que o gráfico de f é côncavo para cima, onde é côncavo para baixo e os seus
pontos de inflexão.
Ver solução completaQuestão 290
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo y);
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
c)
Ver solução completaQuestão 291
(a) Faça um esboço da representação geométrica dos planos cujas equações gerais são dadas por:
(i) x = 2; (ii) y + 1 = 0; (iii) z + 4 = 0; (iv) x − z = 0; (v) 2x + 3y + 4z − 12 = 0.
Ver solução completaQuestão 292
(b) Dê a equação paramétrica para cada um dos três planos coordenados.
(i) x = 2; (ii) y + 1 = 0; (iii) z + 4 = 0; (iv) x − z = 0; (v) 2x + 3y + 4z − 12 = 0.
Ver solução completaQuestão 293
c) Dê a equação geral para cada um dos três planos coordenados.
(i) x = 2; (ii) y + 1 = 0; (iii) z + 4 = 0; (iv) x − z = 0; (v) 2x + 3y + 4z − 12 = 0.
Ver solução completaQuestão 294
Sejam I um intervalo aberto de R e uma curva diferenciável. Mostre que, se existe C ∈ R tal que , para todo t ∈ I, então γ(t) é ortogonal a γ’ (t), para todo t ∈ I. Vale a recíproca? Interprete geometricamente.
Ver solução completaQuestão 295
Considere a curva plana dada por
Esboce a imagem da curva e o sentido do percurso. Sugestão: tente calcular em alguns pontos e ver se consegue visualizar a curva e o sentido do percurso, depois cheque usando algum aplicativo: desmos ou wolframalpha ou outro. O nome dessa curva é “caridióide” - você vai entender a razão!
Ver solução completaQuestão 297
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
f)
Ver solução completaQuestão 298
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
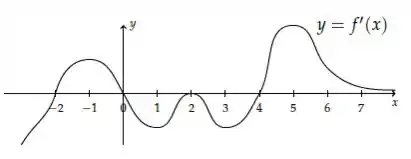
- Admitindo que , faça um esboço do possível gráfico de
Questão 312
18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
c)
Ver solução completaQuestão 313
18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
e)
Ver solução completaQuestão 316
Na função a seguir calcule
Seus Intervalos de D onde f é crescente e onde f é decrescente.
Extremos relativos (locais) e absolutos (globais) de f.
Intervalos em que o gráfico de f é côncavo para cima, onde é côncavo para baixo e os seus
pontos de inflexão.
Ver solução completaQuestão 317
Na função a seguir calcule
Seu domínio, sua paridade, e as assíntotas verticais e horizontais
Ver solução completaQuestão 318
Faça o esboço do traço de cada curva parametrizada abaixo indicando a sua orientação:
(c)
Ver solução completaQuestão 320
Seja a interseção das regiões .
a) As fronteiras de respectivamente, são superfícies quádricas, identifique cada uma delas.
b)Faça um esboço da região
Ver solução completaQuestão 324
Representar graficamente, no plano cartesiano, o produto cartesiano nos seguintes casos: