Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 34

Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for 10   m , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado nos fala de uma janela que tem a forma de um retângulo tendo em cima um semicírculo com perímetro igual a 10   m e pede pra a gente calcular as dimensões da janela que deixaria passar a maior quantidade de luz possível, ou seja, a maior área possível!

Vamos desenhar um esquema pra ficar mais claro:

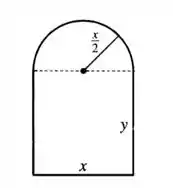
Esse é um problema de maximização, portanto, vamos precisar escrever uma expressão que relaciona a área da janela com suas dimensões e calcular A ' = 0 . Vamos colocar a mão na massa?!

Passo 2

A área da janela pode ser calculada por:

A = x y + π r 2 2

O que fizemos foi somar a área de um retângulo com um semicírculo. Sabemos que r = x 2 pois o enunciado diz que o diâmetro do semicírculo é igual à largura do retângulo. Então:

A = x y + 1 2 π x 2 2

A = x y + x 2 π 8

A outra informação que a gente tem é o perímetro de 10   m , aí dá pra anotar mais uma fórmula:

P = x + 2 y + 2 π r 2 = 10

x + 2 y + π x 2 = 10

Podemos isolar o y nessa equação, assim:

2 y = 10 - x - π x 2

y = 5 - x 2 - π x 4

Substituindo y   em A :

A = x y + x 2 π 8

A = x 5 - x 2 - π x 4 + x 2 π 8

Aplicando a distributiva no produto:

A = 5 x - x 2 2 - x 2 π 4 + x 2 π 8

Temos então:

A = 5 x - x 2 2 - x 2 π 8

Passo 3

Vamos derivar A com relação a x e calcular A ' = 0 para encontrar os pontos críticos da função:

A = 5 x - x 2 2 - x 2 π 8

Assim, derivando, temos:

A ' x = 5 - x - 1 4 π x

Colocando x em evidência:

A ' x = 5 - x 1 + 1 4 π

Igualando esse resultado a zero, vamos ter:

5 - x 1 + 1 4 π = 0

x = 5 1 + 1 4 π

x = 20 4 + π

Achamos x , agora substituindo em y , temos:

y = 5 - x 2 - π x 4

y = 5 - 20 2 4 + π - π   20 4 4 + π

Tirando o MMC:

y = 5 - 10 4 + π - 5 π 4 + π

y = 10 4 + π

Prontinho! Podemos constatar, a altura do retângulo é metade de sua largura.

Valeu, galera! Até a próxima! 😉

Resposta

Dimensões da área máxima: x = 20 4 + π e y = 10 4 + π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 35 a 39, uma partícula está se movendo ao longo de uma reta, de acordo com a equação dada, onde s (m) é a distância orientada entre a posição da partícula e a origem no instante t (s
Nos exercícios de 40 a 45, uma partícula está se movendo ao longo de uma reta, de acordo com a equação de movimento dada, onde s cm é a distância orientada entre a partícula e a origem no instante t s
Nos Exercícios de 35 a 39, uma partícula está se movendo ao longo de uma reta, de acordo com a equação dada, onde s (m) é a distância orientada entre a posição da partícula e a origem no instante t (s
Nos Exercícios de 35 a 39, uma partícula está se movendo ao longo de uma reta, de acordo com a equação dada, onde s (m) é a distância orientada entre a posição da partícula e a origem no instante t (s
Nos Exercícios 33 e 34, uma partícula está se movendo ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância orientada da partícula até a origem, v cm/s é a velocidade